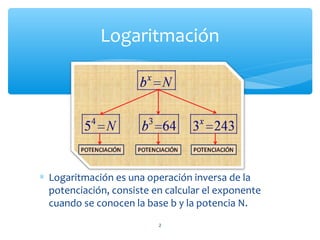
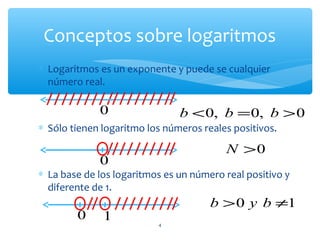
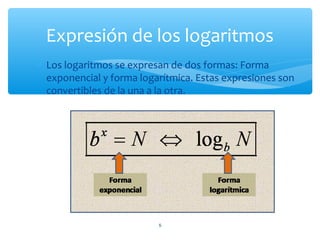
El documento explica las propiedades de los logaritmos. Define logaritmos como la operación inversa a la potenciación, donde el exponente es el logaritmo de la base elevada a la potencia. Luego detalla 7 propiedades generales de los logaritmos, incluyendo que el logaritmo de un producto es la suma de los logaritmos de los factores, y el logaritmo de un cociente es la diferencia de los logaritmos. También cubre cambios de base y otras propiedades complementarias.

1. LOGARITMOS

2. Logaritmación
2
∗ Logaritmación es una operación inversa de la
potenciación, consiste en calcular el exponente
cuando se conocen la base b y la potencia N.

3. Definición de logaritmo
3
∗ Logaritmo de un número
positivo N en una base b,
positiva y diferente de 1, es
el exponente x al cual debe
elevarse la base para
obtener el número N.

4. Conceptos sobre logaritmos
4
∗ Logaritmos es un exponente y puede se cualquier
número real.
∗ Sólo tienen logaritmo los números reales positivos.
∗ La base de los logaritmos es un número real positivo y
diferente de 1.
0
0, 0, 0b b b< = >
10
0
0N >
0 1b y b> ≠

5. Expresión de los logaritmos
5
∗ Los logaritmos se expresan de dos formas: Forma
exponencial y forma logarítmica. Estas expresiones son
convertibles de la una a la otra.

6. Identidad fundamental de los
logaritmos
6
∗ Si el logaritmo de un número es exponente de su propia
base, entonces es igual número N.
Ejemplos.
4
2008
log 6
log 1500
1) 4 6
2) 15002008
=
=

7. Propiedades generales de los
logaritmos
7
1) El logaritmo de 1, en cualquier base, es igual a cero.
Ejemplos:
5
7
1)log 1 0
2)log 1 0
=
=

8. Propiedades generales de los
logaritmos
8
2) El logaritmo de la base es igual a la unidad.
Ejemplos:
6
2
1) log 6 1
2) log 2 1
=
=

9. Propiedades generales de los
logaritmos
9
3) El logaritmo de un producto es igual a la suma de los
logaritmos de los factores.
Ejemplos:
2 2 2
5 5 5
1) log 7 5 log 7 log 5
2) log 25 4 log 25 log 4
× = +
× = +

10. Propiedades generales de los
logaritmos
10
4) El logaritmo de un cociente es igual al logaritmo del
dividendo menos el logaritmo del divisor.
Ejemplos:
2 2 2
5 5 5
1
1) log log 1 log 6
6
10
2) log log 10 log 5
5
 
= − ÷
 
 
= − ÷
 

11. Propiedades generales de los
logaritmos
11
5) El logaritmo de una potencia es igual al exponente por el
logaritmo de la base.
Ejemplos:
3
2 2
4
5 5
1) log 6 3log 6
2) log 5 4log 5
=
=

12. Propiedades generales de los
logaritmos
12
6) El logaritmo de una raíz es igual al logaritmo del
radicando dividido entre el índice.
Ejemplos:
3
3
4 5
5
log 12
1) log 12
2
log 6
2) log 6
4
=
=

13. Propiedades generales de los
logaritmos
13
7) El producto de dos logaritmos recíprocos es igual a la
unidad.
Ejemplos:
2 5
32
1) log 5 . log 2 1
2) log 3 . log 2 1
=
=

14. Propiedades complementarias de los
logaritmos
14
3) Cambio de base.
Ejemplos.
5
2
5
3
6
3
log 3
1) log 3
log 2
log 21
2) log 21
log 6
=
=