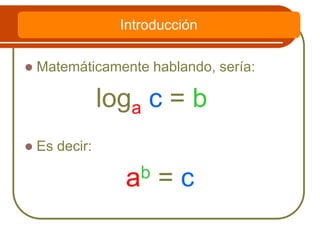
Este documento explica los logaritmos, incluyendo su definición como la función inversa de la función exponencial y algunas de sus propiedades más importantes, como que el logaritmo de la base es igual a uno, el logaritmo de uno en cualquier base es cero, y el logaritmo de un producto es igual a la suma de los logaritmos de sus factores. También cubre los logaritmos decimales y neperianos y algunos ejemplos de aplicación de las propiedades.

1. LOGARITMOS
Srta. Yanira Castro Lizana

2. Definición:
 En términos sencillos y claros, un
logaritmo es un exponente o potencia,
a la que un número fijo (llamado base),
se ha de elevar para dar un cierto
número.
 Entonces, el logaritmo es la función
inversa de la función exponente.
Introducción

3.  Matemáticamente hablando, sería:
loga c = b
 Es decir:
ab = c
Introducción

4.  Ejemplos:
- Log3 81 = 4
es decir: 34 = 81
- Log2 256 = 8
es decir: 28 = 256
- Log4 16 = 2
es decir: 42 = 16
Introducción

5.  Hay ciertas propiedades que debes
conocer de los logaritmos.
 Veremos las más importantes a
continuación.
Propiedades de los logaritmos

6.  El logaritmo de la base siempre es igual
a uno, es decir:
loga a = 1
 Ejemplos:
log5 5 = 1
log89 89 = 1
Log12.500 12.500 = 1
Propiedad 1

7.  El logaritmo de 1 en cualquier base es
siempre igual a cero:
loga 1 = 0
 Ejemplos:
log3 1 = 0
log2a 1 = 0
log43 1 = 0
Propiedad 2

8.  El logaritmo de un producto es igual a la
suma de los logaritmos de sus factores:
loga (b·c) = loga b + loga c
 Ejemplos:
log2 (3·5) = log2 3 + log2 5
log3 (6·2·5) = log3 6 + log3 2 + log3 5
log4 (16·4) = log4 16 + log4 4 = 2+1 =3
Propiedad 3

9.  El logaritmo de una fracción es igual a
la resta del logaritmo del numerador
menos el logaritmo del denominador.
loga (b/c) = loga b – loga c
 Ejemplo:
log2 3 / 4 = log2 3 – log2 4
log4 (16/4) = log4 16 - log4 4 = 2-1 = 1
Propiedad 4

10.  El logaritmo de una potencia es igual a
la potencia multiplicando al logaritmo de
la base de la potencia:
loga bc = c loga b
 Ejemplo:
log2 53 = 3 log2 5
log3 √5 = ½ log3 5
Propiedad 5

11.  El logaritmo de la base elevado a una
potencia es igual a la potencia.
Loga ab = b
 Ejemplo:
log3 32 = 2
log4 46 = 6
log2 23 = 3
Propiedad 6

12. Cambio de base de logaritmo:
 El logaritmo en base a un número es
igual a la fracción entre el logaritmo del
primer número con base en un tercer
número y el logaritmo del segundo
número con base en un tercer número.
loga b = logc b / logc a
 Ejemplo:
log2 8 = log3 8 / log3 2
Propiedad 7

13.  Un número elevado al logaritmo con
base en el mismo número, es igual al
número del logaritmo.
a log
a
b = b
 Ejemplo:
4 log
4
3 = 3
20 log
20
4 = 4
b log
b
2 = 2
3 log
3
5 = 5
Propiedad 8

14. IMPORTANTE
Cuando la base es a = 10, se llaman
logaritmos decimales y se expresan por log en
vez de log10 , es decir:
Cuando la base es a = e, se llaman logaritmos
neperianos y se expresan por ln o L en vez de
loge , es decir:
mlogmlog10
elog m lnm Lm

15. Casos especiales:

16. Ejemplos.
2
porque 100 10
4
porque 9 ( 3)
31
porque 10
1000
3
1
porque 8
2
1
porque e e
4
porque 81 34
log 100 2
3
log 9 4
1
log
1000
3
ln e 1
3log 81
1
2
log 8 3

17. Calcular por la definición de logaritmo el valor de y :