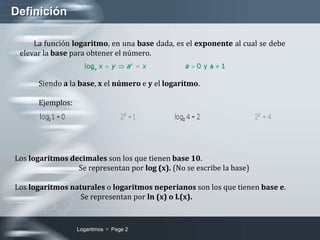
Este documento explica la función logarítmica. Define los logaritmos decimales y naturales, y sus propiedades clave como que no existen logaritmos de números negativos o cero. Explica cómo usar las propiedades de los logaritmos, como que el logaritmo de un producto es la suma de los logaritmos de los factores, para resolver ecuaciones logarítmicas. Incluye ejemplos numéricos de cálculos con logaritmos y resolución de ecuaciones logarítmicas.

1. FUNCION LOGARITMICAEscuela Preparatoria Federal por Cooperación “Antonio Audirac“Resolución de EcuacionesMATEMATICAS IVProfesor: Juan Manuel Lovera

2. Logaritmos  Page 2DefiniciónLa función logaritmo, en una base dada, es el exponente al cual se debe elevar la base para obtener el número.Siendo a la base, x el número e y el logaritmo.Ejemplos: Los logaritmos decimales son los que tienen base 10. Se representan por log (x). (No se escribe la base)Los logaritmos naturales o logaritmos neperianos son los que tienen base e. Se representan porln (x) o L(x).

3. LogaritmosPage 3DefiniciónDe la definición de logaritmo podemos deducir:No existe el logaritmo de un número con base negativa.No existe el logaritmo de un número negativo.No existe el logaritmo de cero.El logaritmo de 1 es cero.El logaritmo en base a de a es uno. El logaritmo en base a de una potencia en base a es igual al exponente.

4. LogaritmosPage 4Propiedades1.- El logaritmo de un producto es igual a la suma de los logaritmos de los factores. 2.- El logaritmo de un cociente es igual al logaritmo del dividendo menos el logaritmo del divisor.3.- El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base.4.- El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz.5.- Cambio de base: esto sirve para realizar cálculos numéricos de los logaritmos

5. LogaritmosPage 5Ecuaciones LogaritmicasLas ecuaciones logarítmicas son aquellas ecuaciones en la que la incógnita aparece afectada por un logaritmo.Para resolver ecuaciones logarítmicas vamos a tener en cuenta:1.- Las propiedades de los logaritmos.2.- 3.- 4.- Además tenemos que comprobar las soluciones para verificar que no tenemos logaritmos nulos o negativos.

6. EjemplosEncontrar el valor numérico de los siguientes logaritmos utilizando la propiedad del cambio de baseTeclea en la calculadora: log (número) 121 ÷ log (número) 2 = LogaritmosPage 6

7. LogaritmosPage 7EjemplosResolver las siguientes ecuaciones logarítmicas:

8. LogaritmosPage 8EjemplosResolver las siguientes ecuaciones logarítmicas:

9. LogaritmosPage 9EjemplosResolver las siguientes ecuaciones logarítmicas: