El documento explica los logaritmos, incluyendo su definición como el exponente al que debe elevarse una base para obtener un número dado. Presenta propiedades como el cambio de base, logaritmos decimales y naturales, y funciones logaríticas. Además, describe aplicaciones de los logaritmos en la escala de Richter y pH.

2. Logaritmo de un número
 El logaritmo en base b de un número a es el número c,
si b elevado al exponente c da como resultado a.
En símbolos: logba = c  bc =a
b es la base del logaritmo y debe ser un número positivo
y distinto de 1.
a es el argumento del logaritmo y debe ser un número
real positivo.

3. Enunciado Expresión simbólica Ejemplo numérico
El logaritmo de 1, en cualquier
base, es 0.
El logaritmo de la base es 1.
El logaritmo de un producto es
igual a la suma de los
logaritmos de los factores, si
éstos existen.
El logaritmo de un cociente es
igual a la resta entre logaritmos
del dividendo y el divisor,
respectivamente, si estos
existen.
El logaritmo de una potencia es
igual al producto del exponente
por el logaritmo de la base.
El logaritmo de una raíz es
igual al logaritmo del radicando
dividido por el índice.
Cambio de base: El logaritmo
en base a de un número se
puede obtener a partir de
logaritmos en otra base.
Corolarios o Consecuencias.

4. C AMBIO DE BASE
 El procedimiento cambio de base nos permite cambiar la base b de
un logaritmo por otras mas conveniente.
Si llamamos c a la base elegida, podemos aplicar directamente la
siguiente formula :
Logab=logcb/logca
Así podemos obtener con la calculadora científica el logaritmo de un
numero en cualquier base.
La nueva base que elegiremos será 10 o e.
Ejemplo: log2256= log256/log2=8 o bien Log2256= ln256/ln2=8

5. Logaritmos decimales: son aquellos de base 10. Generalmente, la base no se
escribe. Por ejemplo:
log x = log10x
El número e: es un número irracional cuyo valor aproximado es:
e = 2,71828
Logaritmos naturales: son los de base e. Se los escribe con ln, es decir que:
ln x =
Logaritmos con la calculadora:
Para obtener logaritmos decimales (en base 10):
pulsamos la tecla log
Para obtener logaritmos naturales o neperianos (en
base e): pulsamos la tecla ln
Para obtener logaritmos en otra base, aplicamos
cambio de base: (ver “Propiedades de los
Logaritmos”)

6. FUNCIÓN LOGARÍTMICA
La función logarítmica se simboliza de la manera:
y=log a X (Se lee: «Logaritmo en base a de X»)
• El dominio de la función Y=log a X es R + , pues coincide con el conjunto
imagen de su inversa y=a X

7. • K > 0 a > 1 b > 0 crece
• K > 0 a > 1 b < 0 decrece
• K > 0 a < 1 b < 0 crece
• K > 0 a < 1 b > 0 decrece
• K < 0 a > 1 b > 0 decrece
• K < 0 a > 1 b < 0 crece
• K < 0 a < 1 b < 0 decrece
• K < 0 a < 1 b > 0 crece
• Desplazamiento horizontal: y = logb(x - a)
• Dominio: (0, ∞); R+
• Imagen: R
• Asíntota vertical: x = a

8. Esta es una representación
de la
función: y=log2x
• El conjunto imagen es R+
• Es creciente en todo su
dominio
• Tiene una asíntota vertical
que es el eje y
• No corta el eje de
ordenadas
• Corta el eje de abscisas en
x=1

9. En este ejemplo podremos ver en qué afectan las diferentes bases en
una función logarítmica. En el gráfico se encuentran dibujadas las
funciones:
f(x)= log2x
G(x)= log3 x
H(x)=log1/2x
J(x)= log1/3x

10. Conclusiones:
Características comunes:
 Cortan al eje de abscisas en el punto (0 ; 1)
 No cortan el eje de ordenadas, y el conjunto imagen es R+
 Tiene una asíntota vertical que es el eje x
Diferencias:
 Si la base es mayor que 1, la función es creciente
 Si la base es menor que 1, la función es decreciente
 Las curvas correspondientes a funciones de bases recíprocas
son simétricas

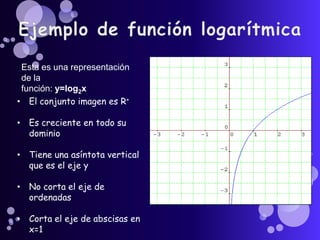
11. En este caso se graficaron las funciones:
f(x) = log2x
Dominio: R+ Asíntota: Eje y
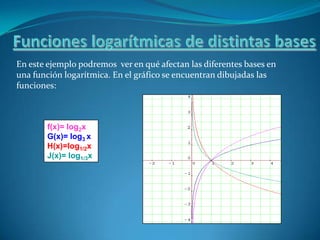
g(x) = log2(x-2)
Dominio: [2;+∞] Asíntota: x = 2
h (x) = log2(x+1)
Dominio: R Asíntota: x = -1
• Si trasladamos el gráfico de f(x) = log2x
dos unidades hacia la derecha, obtenemos
el gráfico de la función g(x) = log2(x-2)
• Si trasladamos el gráfico de f(x) = log2x
una unidad hacia la izquierda, obtenemos el gráfico de la función h(x) = log2(x+1)
• El desplazamiento horizontal, en estos casos, modifica el dominio de la función y
la asíntota.

12. En todos los casos en que se aplican las
funciones exponenciales, como los
expuestos anteriormente, son necesarios lo
logaritmos para averiguar los valores de las
variables que aparecen como incógnitas en
los exponentes

13. La escala de Ritcher, utilizada para medir la intensidad
de los terremotos, es una escala logarítmica de base 10.
La magnitud de un terremoto en esa escala está dada
por la fórmula:
M = log p
Donde M es el grado de la escala de Ritcher y p es la
potencia, que indica cuántas veces mayor fue la
amplitud de la onda sísmica del terremoto en
comparación con una onda de referencia
correspondiente a la situación normal.

14. La concentración de iones hidrógeno en
una solución determina su grado de
acidez. Como se trata de cantidades muy
pequeñas, se inventó una escala
logarítmica que facilita su manejo.
La fórmula que relaciona el pH de una
solución con la concentración de iones
hidrógeno es la siguiente: pH = log
(1/[H+]), donde [H+] representa los moles
de iones hidrógeno por litro.

15. BIBLIOGRAFÍA
 Matemática 2 - Santillana
– Serie Perspectivas
 Matemática 1 – Santillana
– Tapa Negra
 Apuntes de clase