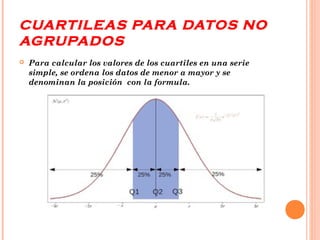
Este documento describe medidas de posición como cuartiles. Los cuartiles dividen un conjunto de datos ordenados en cuatro partes iguales, con el primer cuartil (Q1) marcando el punto por debajo del cual se encuentra el 25% inferior de los datos y el tercer cuartil (Q3) marcando el punto por encima del cual se encuentra el 25% superior. Existen nueve métodos para calcular cuartiles en datos no agrupados, por lo que es importante indicar el método utilizado.

1. TEMA:
MEDIDAS DE
POSICION:CUARTILE
S

2. MEDIDAS DE POSICIÓN
 las medidas de posición son medidas que permiten dividir el
conjunto de datos en partes porcentuales e iguales. Las mas
utilizadas son: los cuartiles y los percentiles.
 Las medidas de dispersión, también llamadas medidas de
variabilidad, muestran la variabilidad de una distribución,
indicando por medio de un número, si las diferentes puntuaciones
de una variable están muy alejadas de la media. Cuánto mayor
sea ese valor, mayor será la variabilidad, cuanto menor sea, más
homogénea será a la media. Así se sabe si todos los casos son
parecidos o varían mucho entre ellos.
 Para calcular la variabilidad que una distribución tiene respecto
de su media, se calcula la media de las desviaciones de las
puntuaciones respecto a la media aritmética. Pero la suma de las
desviaciones es siempre cero, así que se adoptan dos clases de
estrategias.

3. CCUUAARRTTIILLEESS
 Los cuartiles son valores de la variable que dividen el conjunto
ordenado de datos en cuatro partes iguales. Cada unas de estas
partes presentan el 25% de tal de los datos.
 Los cuartiles son tres y se simbolizan como Q1, Q2, y Q3
 Los cantiles son puntos tomados a intervalos regulares de la
función de distribución de una variable aleatoria.
 El término cantil fue usado por primera vez por Kendos cantiles
son puntos tomados a intervalos regulares de la función de
distribución de una variable aleatoria.
 El término cantil fue usado por primera vez por Kendall en 1940.
El cantil de orden p de una distribución (con 0 < p < 1) es el valor
de la variable que marca un corte de modo que una proporción.

4. CUARTILEAS PARA DATOS NO
AGRUPADOS
 Para calcular los valores de los cuartiles en una serie
simple, se ordena los datos de menor a mayor y se
denominan la posición con la formula.

5. EJEMPLOS:

6. CUARTILES PARA DATOS
AGRUPADOS
 En el cálculo de cantiles con distribuciones de
variable continua (por ejemplo, con datos agrupados)
puede conseguirse fácilmente que las partes en que se
divide la distribución sean exactamente iguales. Sin
embargo, en las distribuciones de variable discreta
(como el caso de datos aislados) debemos
conformarnos con que estas partes sean
aproximadamente iguales. Por desgracia, no hay
consenso sobre la forma en que realizar esta
aproximación, existiendo en la literatura científica
nueve métodos diferentes, que conducen a resultados
diferentes. Por ello, al calcular cualquier cuartil de
datos no agrupados por medio de calculadora,
software o manualmente, es básico el saber e indicar
el método utilizado.

7. EJEMPLOS DE
CUARTILES AGRUPADOS

8. DATOS AGRUPADOS
 Los datos agrupados son un término
estadístico usado en análisis de datos. Un grupo
de datos crudo puede ser organizado
construyendo una tabla que muestra la
distribución de frecuencia de la variable (cuyos
valores se dan en el grupo de datos crudo). Tal
tabla de la frecuencia se refiere a menudo como
datos agrupados.

9. EJEMPLOS
 Los datos antedichos se pueden organizar en una
distribución de frecuencia (o datos agrupados) de
varias maneras. Un método es utilizar intervalos
como base.
 El valor más pequeño de los datos antedichos es 8
y el más grande es 34. El intervalo a partir del 8
a 34 está quebrado para arriba en su intervalos
más pequeños (llamados los intervalos de clase).
Para cada intervalo de clase, la cantidad de
elementos de datos que caen en este intervalo se
cuenta. Este número se llama la frecuencia de
ese intervalo de clase. Los resultados se tabulan
como tabla de la frecuencia.

10. IMÁGENES
 Nombre:Hugo Adiel Martínez Villegas