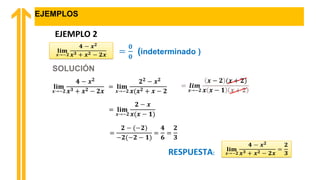
El documento aborda el cálculo de límites en matemáticas, específicamente en formas indeterminadas como 0/0 y límites al infinito, aplicando estos conceptos a problemas de gestión empresarial. Se incluyen ejemplos y ejercicios prácticos para ayudar a los estudiantes a entender y resolver estas situaciones. Además, se discute la importancia de la metacognición y se proporcionan referencias bibliográficas para profundizar en el tema.

1. UPN, PASIÓN POR TRANSFORMAR VIDAS
MATEMÁTICA BÁSICA
LÍMITES INDETERMINADOS E
INFINITOS
Departamento de Ciencias

2. • Factorización.
• Racionalización.
• Simplificaciones de expresiones
algebraicas.
SABERES PREVIOS

3. LOGRO DE LA SESIÓN
Al finalizar la sesión, el estudiante resuelve y
aplica la teoría de límites de la forma 0/0
y límites al infinito en la solución de problemas
relacionados a la gestión empresarial,
interpretándola correctamente.

4. CONTENIDOS
1.-Cálculo de límites de la forma 0/0
2.-Límites al infinito
3.-Metacognición
4.-Referencia Bibliográfica

5. Primer Paso:
o Evaluar el límite por sustitución.
Segundo Paso
Si es posible levantar la indeterminación , a través de
operaciones algebraicas; factorización , productos notables,
racionalización.

6. EJEMPLOS
EJEMPLO 1
SOLUCIÓN
RESPUESTA:

7. EJEMPLOS
EJEMPLO 2
SOLUCIÓN
RESPUESTA:
= 𝒍𝒊𝒎
𝒙→−𝟐
𝒙 − 𝟐 (𝒙 + 𝟐)
𝒙 𝒙 − 𝟏 𝒙 + 𝟐

8. EJEMPLOS
EJEMPLO 3
SOLUCIÓN
RESPUESTA:
= 𝒍𝒊𝒎
𝒙→𝟑
𝒙 𝒙 − 𝟑
𝒙 − 𝟑 𝒙 + 𝟑

9. 10 000
0.001
0.00001
100000
0.0001
-1000
-10000
-100000
1 000 0.001
10 000 0.0001
100 000 0.00001
x
y
-1 000 -0.001
-10 000 -0.0001
-100 000 -0.00001
-0.001
-0.0001
-0.00001
1000
2. LÍMITES AL INFINITO

10. 2. LÍMITES AL INFINITO
Respuesta: 0
I. EL GRADO DEL NUMERADOR ES MENOR AL GRADO DEL DENOMINADOR
Solución: Se divide al numerador y denominador por la variable con su mayor exponente
que aparezca en el denominador.
FORMA
INDETERMINADA:

11. FORMA
INDETERMINADA:
Respuesta: 2
II. EL GRADO DEL NUMERADOR ES IGUAL AL GRADO DEL DENOMINADOR
Solucion: Se divide al numerador y denominador por la variable con su mayor exponente.
2. LÍMITES AL INFINITO

12. FORMA
INDETERMINADA:
III. EL GRADO DEL NUMERADOR ES MAYOR AL GRADO DEL DENOMINADOR
Solucion: Se divide al numerador y denominador por la variable con su mayor exponente.
2. LÍMITES AL INFINITO

13. ¡Recuerda, cada desafío es una oportunidad para aprender!

14. 2. LÍMITES AL INFINITO
Teorema del límite del cociente de polinomios:
EJEMPLOS:
Solución: Solución:
Solución:
lim
𝑥→∞
4𝑥3
2𝑥2
= ∞

15. 2. LÍMITES AL INFINITO
1
2
3
4
5
6
7
8
9
Aplicando el Teorema del límite del cociente de polinomios, calcule los siguientes límites:
EJERCICIOS: LÍMITES AL INFINITO

16. EJERCICIOS: LÍMITES AL INFINITO
1. Determine el siguiente límite: 2. Determine el siguiente límite:
2. LÍMITES AL INFINITO
lim
𝑥→∞
𝑥2
− 7𝑥 + 3 lim
𝑥→−∞
6𝑥3
+ 5𝑥2
− 2

17. BALANCE A LARGO PLAZO
El balance económico mensual, en miles de dólares, de una compañía
vinícola viene dado por:
donde 𝑥 es el precio, en dólares, de una botella de vino. ¿A cuánto tienden
sus ganancias o pérdidas a largo plazo?
( )
2
5
3
+
−
=
x
x
b

18. ¡Recuerda, cada desafío es una oportunidad para aprender!

19. METACOGNICIÓN
1. ¿Qué aprendí de esta sesión?
2. ¿Para que me sirve conocer el uso de los límites?
3. ¿En qué aspectos de tu vida crees que aparece el límite
de una función?

20. REFERENCIAS
N° CÓDIGO AUTOR TÍTULO PAG
1 510 HAEU Haeussler, Ernest.
Matemáticas para administración y
economía.
381-398
2
510 ARYA
2009
Arya, Jagdish
Matemática Aplicada a la
administración y a la economía.
450-460
3 515.15 LARS
Larson, Ron /
Hostetler,Robert /
Edwards, Bruce
Cálculo 41-80

21. GRACIAS