Este documento explica diferentes tipos de inecuaciones, incluyendo inecuaciones cuadráticas, racionales e inecuaciones con valor absoluto. Las inecuaciones cuadráticas pueden tener uno o dos intervalos de solución y requieren factorización. Las inecuaciones racionales son cocientes de expresiones algebraicas. Las inecuaciones con valor absoluto tienen propiedades específicas dependiendo de si el valor absoluto es menor, menor o igual, mayor o mayor o igual a un valor. Se proveen ejemplos resueltos de cada tipo.

2. INECUACIONES CUADRÁTICAS

3. INECUACIONES CUADRATICAS
Las inecuaciones cuadráticas son aquellas cuya expresión es de grado 2, y pueden tener uno o dos intervalos de
solución. Regularmente en una inecuación cuadráticas se deben utilizar elementos algebraicos como la
factorización para dar solución a esta
Ejemplo 4.
Hallar la solución a la siguiente inecuación
x2 – 6x +8 > 0
Solución
x2 – 6x +8 > 0
(x-4)(x-2)>0
Para que esta expresión sea > 0 debe cumplirse
(x – 4) > 0 , ˄ (x – 2) > 0 , ˅ , (x – 4) < 0 , ˄ (x – 2) < 0
x > 4 , ˄ x > 2 , ˅ , x < 4 , ˄ x < 2

4. La primera x > 4 , ˄ x > 2 tendrían como solución
x > 4 que seria la intersección de las dos expresiones x>4 y x>2
Los intervalos de solución entonces serian
(-∞ , 2) ᴜ (4 , ∞ )
La segunda x < 4 , ˄ x < 2 tendrían como solución
x < 2 que seria la intersección de las dos expresiones x<4
y x<2
De esta expresión se puede separar en dos inecuaciones

5. INECUACIONES RACIONALES
Las inecuaciones racionales son aquellas que son el cociente de dos expresiones algebraicas,
Ejemplo 4.
Hallar la solución a la siguiente inecuación
(x – 3)/(x – 2) > 0
La expresión es posible convertirla en
(x – 3).(x – 2) > 0 con x diferente de 2, debido que x-2 está en el denominador
Se igualan cada termino de la expresión a cero para terminar extremos en la solución así:
x – 3 = 0 y x – 2 = 0
De donde X = 3 V X = 2
Solución
(x – 3)/(x – 2) > 0
Se traza la recta real y se segmenta con estos puntos colocándoles los signos + y - de manera alterna iniciando
con el signo positivo

6. Para la solución se toma las que toman los intervalos que contienen el signo positivo sin tomar los extremos
debido que el signo de la inecuación es >
Entonces la solución será
(-∞ , 2 ) U (3 , ∞)
En notación de conjunto será
S={ x/ X<2 v X>3}

7. INECUACIONES CON VALOR ABSOLUTO
Las inecuaciones con valor absoluto, son desigualdades que cumplen con las siguientes propiedades
ǀ x ǀ < a si y solo si -a < x < a
ǀ x ǀ ≤ a si y solo si -a ≤ x ≤ a
ǀ x ǀ > a si y solo si x > a , ˅ , x < -a
ǀ x ǀ ≥ a si y solo si x ≥ a , ˅ , x ≥ -a

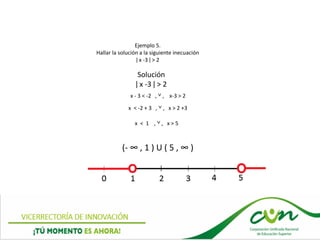
8. Ejemplo 5.
Hallar la solución a la siguiente inecuación
ǀ 2x -3 ǀ ≤ 5
Solución
ǀ 2x -3 ǀ ≤ 5
[-1 , 4 ]
-5 ≤ 2x -3 ≤ 5
-5 + 3 ≤ 2x ≤ 5 + 3
-2 ≤ 2x ≤ 8
-2/2 ≤ x ≤ 8/2
-1 ≤ x ≤ 4

9. Ejemplo 5.
Hallar la solución a la siguiente inecuación
ǀ x -3 ǀ > 2
Solución
ǀ x -3 ǀ > 2
(- ∞ , 1 ) U ( 5 , ∞ )
x - 3 < -2 , ˅ , x-3 > 2
x < -2 + 3 , ˅ , x > 2 +3
x < 1 , ˅ , x > 5

10. BIBLIOGRAFIA
• Calculo; Jorge B. Thomas Jr;
• Calculo Diferencial, Jorge Luis Gil Sevilla;