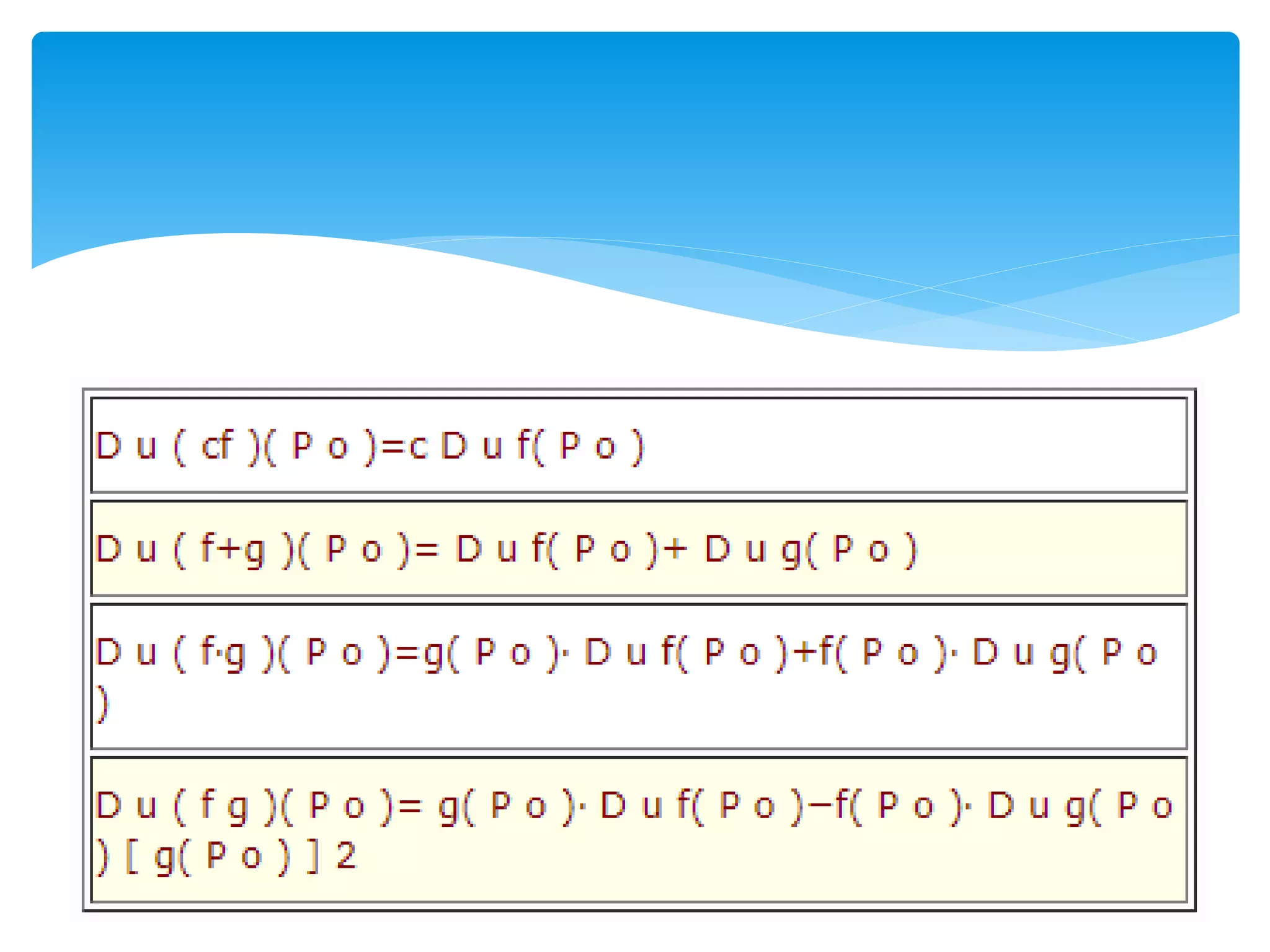
Este documento define y explica el concepto de derivada direccional. Explica que la derivada direccional representa la tasa de cambio de una función en una dirección dada y generaliza las derivadas parciales. Proporciona la fórmula para calcular la derivada direccional en un punto y da algunas propiedades como que la derivada direccional existe cuando las derivadas de funciones combinadas (suma, producto, cociente) existen. Finalmente, presenta un ejemplo numérico para calcular la derivada direccional en un punto.

1. Republica Bolivariana de Venezuela Ministerio del Poder
Popular para la Educación Superior
Instituto Universitario Politécnico Santiago Mariño
San Cristóbal – Edo Táchira
Realizado por:
Erick Samuel Giraldo Castellanos
C.I. 23,136,795

2. Representa la tasa de cambio de la función en la
dirección de dicho vector. Este concepto generaliza las
derivadas parciales, puesto que estas son derivadas
direccionales según la dirección de los respectivos ejes
coordenados.
Concepto

3. Una dirección en ℝ n es cualquier vector de norma 1.
Nota: Si u → es una dirección en el plano ℝ 2 (n=2)
entonces se puede expresar
como u → =( cos⁡ϕ,senϕ ) siendo ϕ el ángulo que
forma el vector con el eje positivo de las X.

4.  Derivada direccional en un punto): Sea f una función
definida en un entorno del punto P o y u → una
dirección. Se define la derivada direccional de f en el
punto P o como el valor del siguiente límite en el caso
de que exista:
lim t→0 f( P o +t u → )−f( P o ) t
 Notación: La derivada direccional se denota
por D u f( P o )= f u ' ( P o )= f φ ' ( P o ) siendo u → =(
cosφ,senφ ) .

5.  Observaciones:
 La existencia de esta derivada direccional significa
que la función de una
variable h( t )=f( P o +t u → ) es derivable en
t=0: D u f( P o )=h'( 0 ) .
 En el caso de una función de dos variables tenemos:
 La derivada direccional en la dirección u → =( 1,0 ) es la
derivada parcial respecto a x
 La derivada direccional en la dirección u → =( 0,1 ) es la
derivada parcial respecto a y.

6.  Sean f y g dos funciones reales de n variables
reales, u → un vector unitario y c un número real.
Entonces si las derivadas direccionales de f y g en la
dirección u → existen en P o entonces las
funciones:
 cf f+g f⋅g f/g (este último caso siempre
que g( P )≠0 próximos a P o ) son derivables en la
dirección u → en el punto P o .
Propiedades de la derivada
direccional

8.  Ejemplo 1.- Dada la
función f( x,y )= x y x 2 + y 2 ∀( x,y )≠(0,0 ) y
f(0,0)=0, determinar, si es que existe, la derivada
direccional en (0,0).
Solución:Aplicando la definición de derivada direccional para la función dada, en el punto (0,0), se
tiene D u f( 0,0 )= lim h→0 f( h cos⁡ϕ,h senϕ )−f( 0,0 ) h = lim h→0 h 2cos⁡ϕ⋅senϕ h 2 ( cos 2 ϕ+
se n 2 ϕ ) h = lim h→0 cos⁡ϕ⋅senϕ h Esta derivada solo existe para las
direcciones u → =( 1,0 ) y u → =(0,1 ) , en las cuales se verifica sen ϕ=0 y cos⁡ ϕ=0 , respectivamente,
es decir, las direcciones de los semiejes X e Y positivos. En esos casos D u f( 0,0 )= f ϕ ' ( 0,0 )=0
Para las demás direcciones no existe la derivada direccional