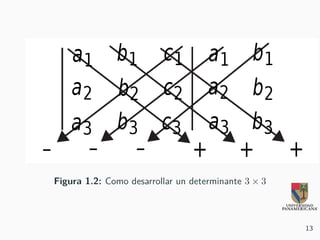
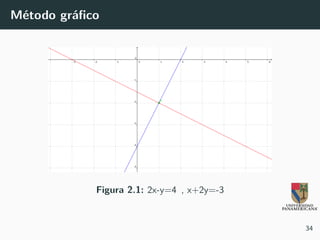
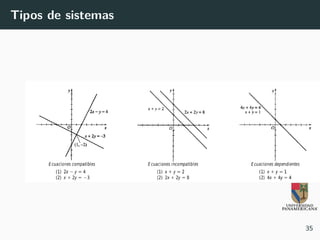
El documento aborda temas de matemáticas básicas centrándose en sistemas de ecuaciones lineales y determinantes, incluyendo ejemplos y métodos de resolución como la regla de Cramer. Se explican condiciones de consistencia e inconsistencia de sistemas de ecuaciones y se presentan ejemplos prácticos para la resolución de situaciones reales, como oferta y demanda. También se discute el cálculo de costo, ingreso y utilidad en contextos económicos.

1. Matemáticas Básicas: Sistemas
Lineales
M. en C. Juliho Castillo
3 de marzo de 2017
ESDAI, Universidad Panamericana
1

2. 1 Determinantes
Determinantes de Segundo Orden
Determinantes de tercer orden
Ejemplos
2 Sistemas de Ecuaciones Lineales Simultáneas
Sistemas de Dos Ecuaciones Lineales
Sistemas de Tres Ecuaciones Lineales
Ejemplos
Oferta y demanda
2

3. Determinantes
3

4. Determinantes
Determinantes de Segundo Orden
4

5. Definición
Definición 1.1.
a b
c d
= ad − bc.
5

6. Ejemplo 1.1.
2 3
−1 −2
=
6

7. Si consideremos el siguiente sistema de ecuaciones



a1x + b1y = c1
a2x + b2y = c2
... (1.1)
7

8. ...y definimos
∆ =
a1 b1
a2 b2
∆x =
c1 b1
c2 b2
∆y =
a1 c1
a2 c2
...
8

9. ...entonces
x =
∆x
∆
y =
∆y
∆
(1.2)
9

10. Ejemplo 1.2.
Resuelva el sistema



2x + 3y = 8
x − 2y = −3
10

11. Determinantes
Determinantes de tercer orden
11

12. Figura 1.1: Determinante 3 × 3
12

13. Figura 1.2: Como desarrollar un determinante 3 × 3
13

14. Ejemplo 1.3.
Desarrolle el siguiente determinante
14

15. Ejemplo 1.4.
Resuelva el siguiente sistema



x + 2y − z = −3
3x + y + z = 4
x − y + 2z = 6
15

16. Determinantes
Ejemplos
16

17. El método de solución de sistemas de ecuaciones linales, por
medio de determinantes, se conoce como Regla de Cramer.
17

18. Ejemplo 1.5.
Resuelva el siguiente sistema por la Regla de Cramer



4x + 2y = 5
3x − 4y = 1
18

19. Ejemplo 1.6.
Resuelva el siguiente sistema por la Regla de Cramer



3u + 2v = 18
−5u − v = 12
19

20. Ejemplo 1.7.
Resuelva el siguiente sistema por la Regla de Cramer



2x + y − z = 5
3x − 2y + 2z = −3
x − 3y − 3z = −2
20

21. Ejemplo 1.8.
Resuelva el siguiente sistema por la Regla de Cramer



x + 2z = 7
3x + y = 5
2y − 3z = −6
21

22. Un sistema de n ecuaciones con n incognitas tiene una única
solución si y solo si su determinante principal ∆ = 0.
En este caso, decimos que el sistema es consistente.
22

23. Un sistema de n ecuaciones con n incognitas tiene una única
solución si y solo si su determinante principal ∆ = 0.
En este caso, decimos que el sistema es consistente.
22

24. Si ∆ = 0, entonces o bien existen multiples soluciones, o bien
no existe alguna en absoluto.
En cualquier caso, decimos que el sistema es inconsistente.
23

25. Determine si 


5x − 2y = 10
10x − 4y = 20
es consistente; y de no ser el caso, explique que sucede con las
soluciones.
24

26. Determine si 


5x + 3y = 15
10x + 6y = 60
es consistente; y de no ser el caso, explique que sucede con las
soluciones.
25

27. Determine si 


x − 3y + 2z = 4
2x + y − 3z = −2
4x − 5y + z = 5
es consistente; y de no ser el caso, explique que sucede con las
soluciones.
26

28. Sistemas de Ecuaciones Lineales
Simultáneas
27

29. Sistemas de Ecuaciones Lineales
Simultáneas
Sistemas de Dos Ecuaciones Lineales
28

30. Supongamos que ai, bi, ci, i = 1, 2 son número dados:



a1x + b1y = c1
a2x + b2y = c2
En el sistema anterior, nuetro objetivos es encontrar dos
números x, y tales que cumplan ambas ecuaciones
simultaneamente.
29

31. Ejemplo 2.1.
La solución del sistema



x + y = 7
x − y = 3
es x = 5, y = 2.
30

32. A continuación, ejemplificaremos algunos de los métodos más
comunes para resolver sistemas de ecuaciones.
31

33. Suma y resta
Ejemplo 2.2.
2x − y = 4 (2.1)
x + 2y = −3 (2.2)
32

34. Método de sustitución
Despejando de (2.1), obtenemos
y = 2x − 4.
Sutituyendo en (2.2), obtenemos
x + 2(2x − 4) = −3.
33

35. Método de sustitución
Despejando de (2.1), obtenemos
y = 2x − 4.
Sutituyendo en (2.2), obtenemos
x + 2(2x − 4) = −3.
33

36. Método gráfico
Figura 2.1: 2x-y=4 , x+2y=-3
34

37. Tipos de sistemas
35

38. Sistemas de Ecuaciones Lineales
Simultáneas
Sistemas de Tres Ecuaciones Lineales
36

39. Supongamos que ai, bi, ci, di, i = 1, 2, 3 son número dados:



a1x + b1y + c1z = d1
a2x + b2y + c2z = d2
a3x + b3y + c3z = d3
En el sistema anterior, nuetro objetivos es encontrar dos
números x, y, z tales que cumplan las ecuaciones
simultaneamente.
37

40. Ejemplo 2.3.
Resuelva
2x + 5y + 4z = 4 (a)
x + 4y + 3z = 1 (b)
x − 3y − 2z = 5 (c)
38

41. Sistemas de Ecuaciones Lineales
Simultáneas
Ejemplos
39

42. Ejemplo 2.4.
2x − y = 4
x + y = 5
40

43. Ejemplo 2.5.
5x + 2y = 3
2x + 3y = −1
41

44. Ejemplo 2.6.
2x + 3y = 3
6y − 6x = 1
42

45. Ejemplo 2.7.
5y = 3 − 2x
3x = 2y + 1
43

46. Ejemplo 2.8.
x − 2
3
+
y + 1
6
= 2
x + 3
4
−
2y − 1
2
= 1
44

47. Ejemplo 2.9.
Encuentre dos números sabiendo que si uno de ellos se suma
con el doble del otro se obtiene 21, y que si este último se
suma con el doble del primero resulta 18.
45

48. Ejemplo 2.10.
Hace seis años, Agustín era 4 veces mayor que Pablo.
Encuentre sus edades actuales sabiendo que dentro de 4 años
sólo será dos veces mayor que Pablo.
46

49. Ejemplo 2.11.
Dos libras de café y 3 kg de mantequilla cuestan $4.20. Al
cabo de 1 mes, el precio del café ha subido 10 % y el de la
mantequilla 20 % de forma que la adquisición de los productos
anteriores cuesta ahora $4.86. Determine el precio original de
cada uno de los productos.
47

50. Ejemplo 2.12.
Si se mezclan 3 galones de aceite del tipo A con 7 galones del
tipo B el precio de la mezcla es de 43 pesos/galón. Sin
embargo, si se mezclan 3 galones del aceite A con 2 galones
del B el precio de la mezcla es de 46 pesos/galón. Encuentre el
precio del galón de cada uno de los tipos de aceite.
48

51. Ejemplo 2.13.
Un inversionista tiene colocado parte de su capital a 3 % y el
resto a 5 % de interés simple, percibiendo anualmente $116 de
intereses. Si aumenta en 25 % el dinero que tiene a 3 % y en
40 % el que tiene a 5 %, sus intereses anuales aumentan en
$41. Calcule el dinero que tiene invertido a cada uno de los
tipos de interés.
49

52. Ejemplo 2.14.
Encuentre 3 números sabiendo que el primero es igual al
segundo más la mitad del tercero, que la suma del segundo y el
tercero es igual al primero más 1, y que si se resta el segundo
de la suma del primero con el tercero el resultado es 5.
50

53. Sistemas de Ecuaciones Lineales
Simultáneas
Oferta y demanda
51

54. El costo total C de un lote de mercancía está dado por
C(q) = C0 + C ∗ q
donde q es el número de unidades, C0 es un costo fijo por lote
y C es el costo marginal, i.e., el costo por unidad.
52

55. El ingreso total I por un lote de mercancía está dado por
I(q) = p ∗ q,
donde p es el ingreso marginal, i.e, el ingreso por unidad
(generalmente el precio unitario de venta), mientras que q es
nuevamente el número de unidades.
53

56. La ganancia (o utilidad) U(q) por un lote de mercancía está
dada por
U(q) = I(q) − C(q) = p ∗ q − (C0 + C ∗ q) ,
o de manera equivalente
U(q) = (p − C ) ∗ q − C0.
54

57. El punto de equilibrio se alcanza cuando los costos son iguales
a los ingresos, es decir,
I(q) = C(q),
o de manera equivalente, cuando la ganancia es nula:
U(q) = I(q) − C(q) = 0.
55

58. Ejemplo 2.15.
Para un fabricante de relojes, el costo de mano de obra y de
los materiales por reloj es de $15 dólares y los costos fijos son
de $2000 dólares al día. Si se vende cada reloj a $20 dólares.
a) ¿Cuántos relojes deberá producir y vender para mantenerse
en el punto de equilibrio? b) ¿Cuántos relojes deberá vender
para tener una utilidad de $3000 dólares?
56

59. Ejemplo 2.16.
2.-El costo total diario de producir manzanas caramelizadas
esta dado por: y = 2.5x + 300.
(a) Si cada manzana se vende a $4 ¿Cuál es el punto de
equilibrio?
(b) Si el precio de venta incremente a $5 ¿Cuál es el nuevo
punto de equilibrio?
(c) Si se sabe que al menos 150 manzanas pueden venderse al
día ¿Qué precio deberá fijarse para garantizar que no haya
pérdidas?
57