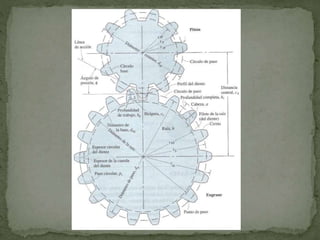
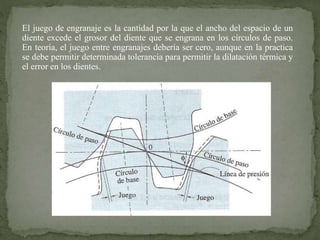
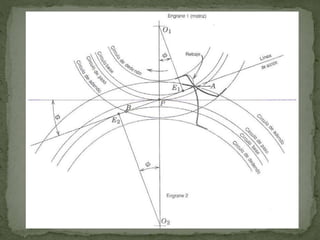
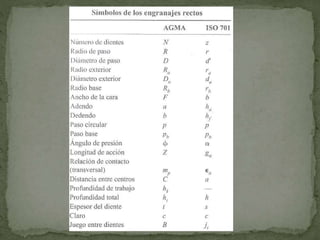
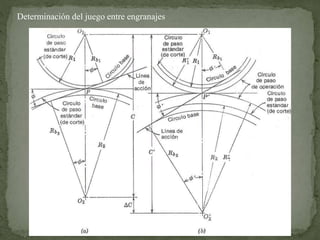
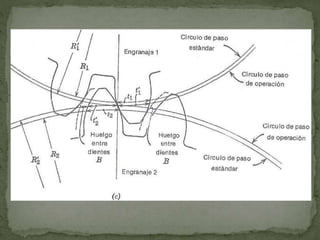
Este documento describe los diferentes tipos de engranes, incluyendo engranes rectos, helicoidales, cónicos y de tornillo sin fin. Explica conceptos clave como el paso circular, el radio de paso, el ángulo de presión y la relación de contacto. También cubre temas como la estandarización de engranes y los cálculos para diseñar engranes que cumplan con ciertos requisitos de velocidad y distancia entre ejes.

1. Catedrático. Juan René González Romero

2. Un engrane se puede considerar como una rueda dentada que cuando
se acopla con otra rueda dentada de diámetro mas pequeño (el piñón),
transmitirá rotación de un eje a otro. La función principal de un
engrane es transferir potencia de un eje a otro, manteniendo una
razón definida entre las velocidades rotacionales de los ejes. Los
dientes de un engrane impulsor empujan los dientes del engrane
impulsado, ejerciendo una componente de la fuerza perpendicular al
radio del engrane. De esta forma se transite un par de torsión y como
el engrane gira, se transmite potencia. Los engranes son transmisores
de par de torsión fuerte y resistente. Su eficiencia de transmisión de
potencia puede ser tan alta como de 98%. Por otro lado, usualmente
los engranes son más costosos que otros transmisores de par de
torsión, tales como los de transmisión por cadena y por banda.

3. Los engranes se dividen en tres clases principales:
 Engranes de eje paralelo
 Engranes no paralelos coplanares
 Engranes no paralelos no coplanares

4. Engranes de ejes paralelos
Los engranes de eje paralelo son el tipo de engrane más simple y
popular. Estos engranes conectan ejes paralelos y pueden transferir
grandes cantidades de potencia con alta eficiencia. En esta clasificación
los engranes rectos y los helicoidales son dos de los principales tipos de
engrane.

5. Engranes rectos
En la figura se observa una transmisión por engranes rectos con los dientes
en el exterior de un cilindro y paralelos al eje del mismo. Los engranes
rectos son los más simples y el tipo más común.

6. Engranes helicoidales
En la figura se muestra una transmisión por engranaje helicoidal, con los
dientes del engrane cortados en una espiral que se envuelve alrededor de
un cilindro. Los dientes helicoidales entran a la zona de acoplamiento
progresivamente y, por lo tanto, tienen una acción más suave que los
dientes de los engranes rectos.

7. Engranes no paralelos coplanares
Se analizan engranes que tienen sus ejes no paralelos y que son
coplanares. Los engranes cónicos, Zerol y espirales se encuentran en la
clase coplanar no paralela. La característica común de esta clase es la
reexpedición de la potencia alrededor de una esquina.

8. Engranes cónicos con dientes rectos

9. Engranes no paralelos no coplanares
Los engranes no paralelos no coplanares son más complejos en geometría
y manufactura que los engranes de las clasificaciones previas. Como
resultado, estos engranes son más caros que los otros engranes analizados.

10. En la figura se muestra esta clase de engrane una transmisión por tornillo
sin fin con dientes cilíndricos. Estos engranes proporcionan relaciones de
reducción considerablemente más altas, pero su capacidad de soporte de
carga es baja, su presión de contacto es bastante alta y su tasa de desgaste
es elevada. Así, las transmisiones por tornillo sin fin sólo sirven para
aplicaciones de carga ligera.

14. Al tener en cuenta dos superficies curvas en contacto directo, se ha
demostrado que la relación de las velocidades angulares es
inversamente proporcional a los segmentos en que se corta la línea de
los centros por la línea de acción o normal común a las dos superficies
en contacto. Si la línea de acción siempre intercepta la línea de los
centros en un punto fijo, entonces la relación de velocidad angular
permanece constante.

16. Involutometría
Los círculos empleados como base
para generar las involutas se conocen
como círculos base y son el corazón
del sistema de engranajes de involutas.
El ángulo comprendido entre una línea
perpendicular a la de acción que pasa
por el centro del circulo base y una
línea desde O1 a Q (u O2 a Q) se
conoce como ángulo de presión de la
involuta. Al punto P se le llama el
punto de paso y los círculos que pasan
por este punto se llaman círculos de
paso o primitivos.

17. Rb es el radio base
ϕ es el ángulo de presión
tan ϕ – ϕ = inv ϕ se llama
función involuta
t es el espesor del diente
Es posible calcular el espesor del diente por medio de la ecuación anterior en
cualquier punto de la involuta, a partir del espesor en cualquier otro punto.

18. El espesor de un diente de un engrane involuta es de 0.314 pulg en un radio
de 3.5 pulg y un ángulo de presión involuta de 14.5°. Calcule el espesor del
diente y el radio en un punto sobre la involuta el cual tiene un ángulo de
presión de 25°.

19. El juego de engranaje es la cantidad por la que el ancho del espacio de un
diente excede el grosor del diente que se engrana en los círculos de paso.
En teoría, el juego entre engranajes debería ser cero, aunque en la practica
se debe permitir determinada tolerancia para permitir la dilatación térmica y
el error en los dientes.

20. Características de la acción de la involuta
En la generación de la involuta se analizó que la normal común a las dos
superficies involutas es tangente a los dos círculos base, a esta normal
común también se le llama la línea de acción.
Se conoce como razón o relación de contacto a la relación del arco de
acción al paso circular. La relación de contacto para los engranajes de
dientes involuta también es igual a la relación de la longitud de acción, o
definido como la distancia desde el inicio al final del contacto medida sobre
la línea de acción, al paso base.

22. El ángulo ϕ se conoce como el ángulo de presión de los dos engranes
engranados y se debe distinguir del ángulo de presión de involuta de
un punto de involuta.
Cuando dos engranes están en contacto en el punto de paso, el ángulo
de presión de los engranes engranados y los ángulos de presión de la
involuta de las dos involutas en contacto en el punto de paso son
iguales.

24. La longitud Z de acción:
Donde:

25. El paso base
Donde:
La relación de contactos mp esta definida por

26. Dos engranes iguales rectos de 48 dientes
engranan con radios de paso de 4 pulg y
addendums de 0.167 pulg. Si el ángulo de presión
es de 14.5°, calcule la longitud Z y la razón de
contacto.

27. Interferencia en los engranajes de involuta
Se menciono que una involuta comienza en el círculo base y se genera
hacia afuera. En consecuencia, es imposible tener involuta dentro del
círculo base. La línea de acción es tangente a los dos círculos base de
un par de engranes acoplados y estos puntos representan los límites
extremos de la longitud de acción. Se dice que estos dos puntos son
puntos de interferencia. Si los dientes tienen una proporción tal que el
inicio del contacto ocurre antes de que se encuentre el punto de
interferencia, entonces la porción involuta del engrane movido se
acopla con una porción no involuta del engrane motriz y se dice que
ocurre una interferencia de involuta.
Cuando hay interferencia de involuta la punta del diente movido rebaja
el flanco del diente motriz.

29. Estandarización de los engranes
La estandarización de los engrane rectos ayudan al desarrollo de
engranes intercambiables. Junto al problema de la intercambiabilidad
se encuentra la forma como se van a cortar los engranes.
Existen varias formas para maquinar los engranes rectos, las más
antigua de las cuales consiste en utilizar una fresa de forma para quitar
el material entre los dientes a medida que el disco para el engrane se
posiciona a lo largo de una revolución completa en una fresadora.

31. El método adoptado en los Estados Unidos consistió en especificar la relación
del número de dientes con respecto al diámetro de paso. A esta relación se le dio
el nombre de paso diametral y se expresa como:
N = número de dientes
D = diámetro de paso, pulg
En Europa, el método de clasificación consiste en especificar la relación del
diámetro de paso con respecto al número de dientes, y a esta relación se le
denomina módulo. Por lo tanto, el módulo es el reciproco del paso diametral y
se expresa como:
D = diámetro de paso, mm
N = número de dientes
m = módulo

32. Debe notarse que el paso diametral y el módulo se definen como relaciones y no
son distancias físicas que se puedan medir en un engrane. El paso circular, por
el contrario, se definió anteriormente como la distancia medida a lo largo del
círculo de paso desde un punto en un diente hasta el punto correspondiente en el
siguiente diente. La relación entre el paso circular y el paso diametral o módulo
puede expresarse como sigue:
en donde:
p = paso circular
Pd = paso diametral
m = módulo

33. La siguiente es una lista de fresas para engranes disponibles comercialmente en
pasos diametrales con ángulos de presión de 14 ½° y 20°.
La siguiente es una lista de fresas estándar en módulo métricos (ángulo de
presión de 20°)

36. Los módulos métricos de la norma británica le corresponden las
siguientes proporciones de dientes:

41. Si los engranes rectos se producen con cortadores estándar, podrán
intercambiarse si se satisfacen las siguientes condiciones:

42. Numero mínimo de dientes para evitar la interferencia
Numero mínimo de dientes para acoplamiento con una cremallera si que haya
rebaje.

43. Determinación del juego entre engranajes

45. En la imagen se muestra el perfil de dos engranes estándar que se acoplan a la
distancia estándar entre centros

49. Un piñón de 18 dientes, paso diametral 8, ángulo de
presión de 25° y profundidad total, conduce un engrane
de 45 dientes. Calcule los radios de paso, los radios de
base, addedum y dedendum y el espesor del diente en el
circulo de paso.

50. Un piñón de 20°, módulo 3, de 24 dientes mueve un
engrane de 60 dientes. Calcule la longitud de acción y la
relación de contacto si los engranes se acoplan sin que
haya juego entre ellos.

51. Dos flechas cuyos ejes se encuentran separados 8.5
pulg, serán acoplados por medio de engranes rectos con
una razón de velocidad angular de 1.5. Utilizando un
paso diametral de 6, seleccione los números de dientes
de dos pares de engranes que mejor se ajusten a los
requerimientos anteriores.

52. Determine las diversas combinaciones de engranes de
20° de profundidad total que se pueden utilizar para
operar a una distancia entre centros de 5 pulg con una
relación de velocidades angulares de 3:1, además
especifique el addendum y dedendum . El paso
diametral no debe ser mayor de 12.