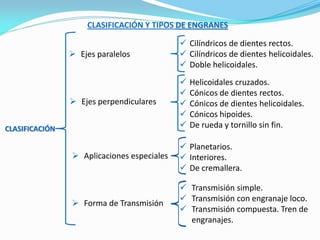
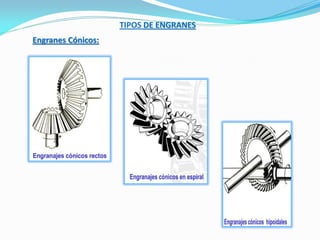
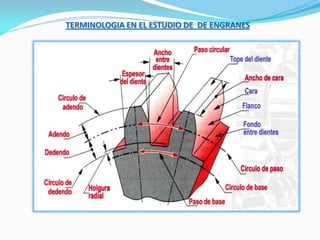
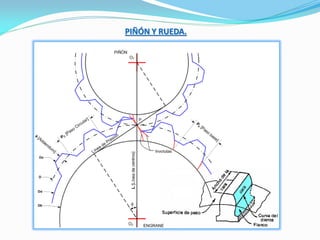
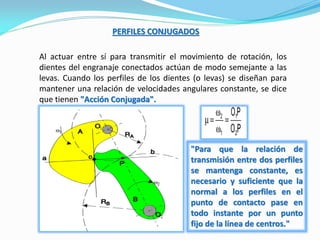
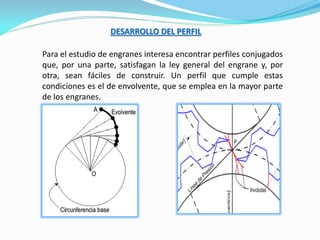
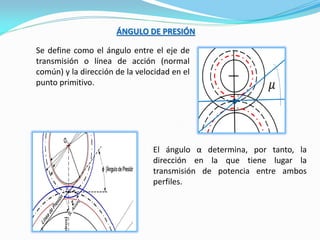
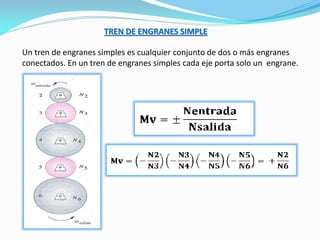
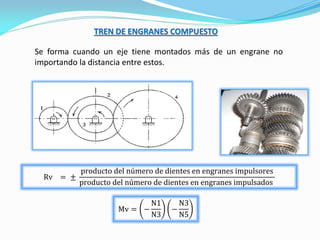
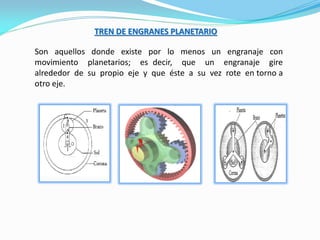
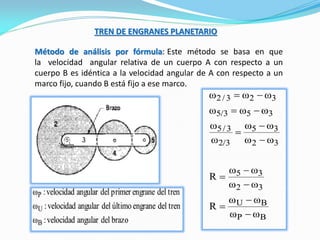
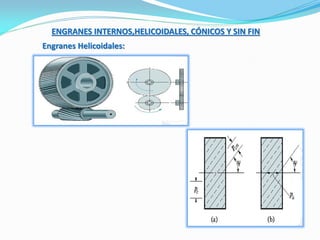
El documento describe los conceptos fundamentales del diseño cinemático de engranajes. Explica los diferentes tipos de engranajes, la clasificación, terminología, relaciones matemáticas que rigen su diseño como el módulo, diámetro primitivo y número de dientes. También cubre conceptos como piñón y rueda, perfiles conjugados, ángulo de presión, trenes de engranajes simples, planetarios y la relación entre las velocidades angulares de dos ruedas engranadas.