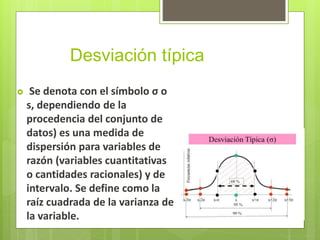
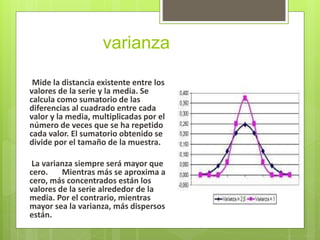
Este documento describe varias medidas de dispersión como el rango, desviación típica, varianza y coeficiente de variación. Explica que las medidas de dispersión cuantifican cuán alejados están los valores de una distribución de su media y que cuanto mayor es el valor de dispersión, mayor es la variabilidad. También proporciona fórmulas y características clave de cada medida.

1. . Republica Bolivariana De Venezuela
Ministerio Del Poder Popular Para La Educación Superior
Instituto Universitario Politécnico
“Santiago Mariño”
Ing. mantenimiento mecánico
Medidas de dispersión
Tutor: Autor:
Ramón Aray Irene García
CI: 25852521

2. medidas de dispersión
También llamadas medidas de variabilidad, muestran la
variabilidad de una distribución, indicando por medio de un
número si las diferentes puntuaciones de una variable están
muy alejadas de la media. Cuanto mayor sea ese valor, mayor
será la variabilidad, y cuanto menor sea, más homogénea
será a la media. Así se sabe si todos los casos son parecidos o
varían mucho entre ellos.
Para calcular la variabilidad que una distribución tiene
respecto de su media, se calcula la media de las desviaciones
de las puntuaciones respecto a la media aritmética. Pero la
suma de las desviaciones es siempre cero, así que se adoptan
dos clases de estrategias para salvar este problema. Una es
tomando las desviaciones en valor absoluto (desviación
media) y otra es tomando las desviaciones al cuadrado
(varianza).

3. características
 Las medidas de dispersión nos sirven para cuantificar la separación de los
valores de una distribución.
 Las medidas de dispersión nos permiten ver el rango entre el cual pudiera
pudiese moverse la variable. De allí radica su importancia ya que es
utilizada para fijar los valores de las variables para lograr una mejor
administración de los procesos: productivos, administrativos, de servicio
etc. En cualquier área donde se puedan generar y tomar datos :educativos
,de salud , comercio, producción, economía entre otros.
 Al calcular una medida de centralización como es la media aritmética,
resulta necesario acompañarla de otra medida que indique el grado de
dispersión, del resto de valores de la distribución, respecto de esta media.
 A estas cantidades o coeficientes, les llamamos: MEDIDAS DE
DISPERSIÓN, pudiendo ser absolutas o relativas.

4. Usos de las medidas de dispersión
 Las medidas de dispersión nos informan sobre
cuanto se alejan del centro los valores de la
distribución.
 Son medidas que se toman para tener la
posibilidad de establecer comparaciones de
diferentes muestras, para as cuales son
conocidas ya medidas que se tienen como típicas
en su clase.

5. Rango
 Es una Medida de Dispersión que indica cómo los datos de
una variable se distribuyen de menor a mayor, es decir la
distancia entre el valor mínimo y máximo, es fácil de
calcular porque solo deberá restar el valor máximo menos
el valor mínimo. El Rango se ve afectado cuando exista
valores muy aislados del grupo, la información que
suministra no dice nada de la distribución de
puntuaciones.
 Ejemplo: Se tienen las edades de 5 estudiantes
universitarios de 1er año a saber: 18,23,21,36,27…
para calcular la medida aritmética (promedio de las
edades, se tiene que) R= xn- xi)=36-18=16 años

6. Características de Rango
 Este se basa en valores extremos, por lo que en
ocasiones tienden hacer errático.
 Debido a que solo considera los valores extremos
siempre existe el peligro del que el recorrido
ofrezca una descripción distorsionada de la
dispersión.
 Cuanto mayor es el rango, mas dispersos están
los datos de un conjunto.
 Se limita su uso a una información inicial.

7. Utilidad del Rango
 Permite obtener una idea de la dispersión de los
datos, cuanto mayor es el rango mas dispersos
están los datos de un conjunto.
 Conserva datos y se puede calcular a partir de
restar el valor mínimo al valor máximo
considerado.
 Utiliza únicamente una pequeña parte de la
información.
 Expresa cuantas unidades de diferencia podemos
esperar ,como máximo, entre dos valores de la
variable.
 El rango estima el campo de variación de la
variable.

8. Desviación típica
 Se denota con el símbolo σ o
s, dependiendo de la
procedencia del conjunto de
datos) es una medida de
dispersión para variables de
razón (variables cuantitativas
o cantidades racionales) y de
intervalo. Se define como la
raíz cuadrada de la varianza de
la variable.

9. Características de desviación típica
 Es el parámetro de dispersión mas utilizado.
 Es afectada por el valor de cada observación.
 Como consecuencia de considerar desviaciones cuadráticas pone
mayor énfasis en las desviaciones extremas que en las demás
desviaciones.
 Al construir la tabla de frecuencia de una variable discreta y
calcular a partir de ella la desviación típica, no hay perdida de
información por lo que la desviación para los datos observados es
igual que para los datos tabulados.
 Si a todos los datos se les suma una constante, la desviación
típica sigue siendo la misma.
 Si todos los datos se les multiplica por una constante , la
desviación típica queda multiplicada por dicha constante.

10. Utilidad de la desviación típica
 su utilidad radica en la transmisión en cuanto
tienden a alejarse los valores concretos del
promedio en una distribución. De hecho
específicamente, el cuadrado de la desviación
típica es “el promedio del cuadrado de la
distancia de cada punto respecto del promedio” .
Se suele representar con una S o con la letra
sigma.

11. varianza
Mide la distancia existente entre los
valores de la serie y la media. Se
calcula como sumatorio de las
diferencias al cuadrado entre cada
valor y la media, multiplicadas por el
número de veces que se ha repetido
cada valor. El sumatorio obtenido se
divide por el tamaño de la muestra.
La varianza siempre será mayor que
cero. Mientras más se aproxima a
cero, más concentrados están los
valores de la serie alrededor de la
media. Por el contrario, mientras
mayor sea la varianza, más dispersos
están.

12. Características de la varianza
 Es siempre un valor no negativo, que puede ser igual o distinta de 0.
 La varianza es la medida de dispersión cuadrática optima por ser la
menor de todas.
 Si a todos los valores de la variable se le suma una constante la
varianza no se modifica.
 Si todos los valores de la variable se multiplican por una constante la
varianza queda multiplicada por el cuadrado de dicha constante.
Usos de la varianza
 Se utiliza para identificar la medida de las desviaciones cuadráticas de
una variable de carácter aleatorio considerando el valor medio de
esta .

13. Coeficiente de variación
 Cuando se desea hacer referencia a la relación entre el tamaño de la
media y la variabilidad de la variable, se utiliza el coeficiente de
variación. Su fórmula expresa la desviación estándar como
porcentaje de la media aritmética, mostrando una mejor
interpretación porcentual del grado de variabilidad que la desviación
típica o estándar. Por otro lado presenta problemas ya que a
diferencia de la desviación típica este coeficiente es variable ante
cambios de origen.
Se calcula:

14. Características coeficiente de
variación.
 Puesto que tanto la desviación estándar como la media se
miden en las unidades originales ,el CV es una medida
independiente de las unidades de medición.
 Debido a la propiedad anterior el CV es la cantidad mas
adecuada para comparar la variabilidad de dos conjuntos de
datos.
 Se calcula como cociente entre la desviación típica y la
media.es un porcentaje que permite comparar el nivel de
dispersión de dos muestras .
 El coeficiente de variación es típicamente menor que 1, sin
embargo en ciertas distribuciones de probabilidad puede ser 1
o mayor que 1.
 Para su mejor interpretación se expresa como porcentaje.

15. Utilidad de coeficiente de
variación.
 El CV es muy usado para evaluar la precisión de un
experimento, comparando en CV del experimento en
cuestión con los valores del mismo en experiencias
anteriores.
 Comparar la variabilidad entre dos grupos de datos
referidos a distintos sistemas de unidades de medida.
Por ejemplo: kilogramos y centímetros.
 Comparar la variabilidad entre dos grupos de datos
obtenidos por dos o mas personas distintas .
 Comparar dos grupos de datos que tienen distinta
medida.

16. Bibliografía
 https://es.wikipedia.org
 http://support.minitab.com/
 http://www.buenastareas.com/
 Introducción a la probabilidad y estadística; 13ª Ed;
Thomson Cengage Learning; México FUENLABRADA, S.
(2000). Probabilidad y Estadística. McGraw-Hill. México