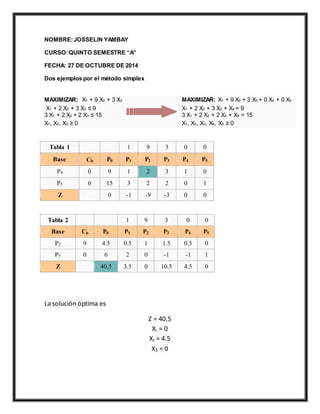
El documento presenta dos ejemplos resueltos del método simplex para problemas de programación lineal de maximización. El primer ejemplo tiene tres variables de decisión y dos restricciones, y la solución óptima es Z=40.5 con X2=4.5 y las demás variables en cero. El segundo ejemplo tiene ocho variables y cinco restricciones, y después de aplicar el método simplex la solución óptima encontrada es Z=11.4285714 con X1=0.45714285714286, X3=1.2571428571429 y las

1. NOMBRE: JOSSELIN YAMBAY
CURSO: QUINTO SEMESTRE “A”
FECHA: 27 DE OCTUBRE DE 2014
Dos ejemplos por el método simplex
MAXIMIZAR: X1 + 9 X2 + 3 X3
MAXIMIZAR: X1 + 9 X2 + 3 X3 + 0 X4 + 0 X5
X1 + 2 X2 + 3 X3 ≤ 9
3 X1 + 2 X2 + 2 X3 ≤ 15
Tabla 1 1 9 3 0 0
Base Cb P0 P1 P2 P3 P4 P5
P4 0 9 1 2 3 1 0
P5 0 15 3 2 2 0 1
Z 0 -1 -9 -3 0 0
Tabla 2 1 9 3 0 0
Base Cb P0 P1 P2 P3 P4 P5
P2 9 4.5 0.5 1 1.5 0.5 0
P5 0 6 2 0 -1 -1 1
Z 40.5 3.5 0 10.5 4.5 0
La solución óptima es
Z = 40.5
X1 = 0
X2 = 4.5
X3 = 0
X1 + 2 X2 + 3 X3 + X4 = 9
3 X1 + 2 X2 + 2 X3 + X5 = 15
X1, X2, X3 ≥ 0 X1, X2, X3, X4, X5 ≥ 0

2. MAXIMIZAR: 3 X1 + 4
X2 + 8 X3
MAXIMIZAR: 3 X1 + 4 X2 + 8 X3 + 0
X4 + 0 X5 + 0 X6 + 0 X7 + 0 X8
4 X1 + 1 X2 + 3 X3 ≤ 8
6 X1 + 2 X2 + 1 X3 ≤ 4
1 X1 + 3 X2 + 6 X3 ≤ 8
3 X1 + 2 X2 + 8 X3 ≤ 12
4 X1 + 6 X2 + 1 X3 ≤ 10
4 X1 + 1 X2 + 3 X3 + 1 X4 = 8
6 X1 + 2 X2 + 1 X3 + 1 X5 = 4
1 X1 + 3 X2 + 6 X3 + 1 X6 = 8
3 X1 + 2 X2 + 8 X3 + 1 X7 = 12
4 X1 + 6 X2 + 1 X3 + 1 X8 = 10
X1, X2, X3 ≥ 0
X1, X2, X3, X4, X5, X6, X7, X8 ≥ 0
 Como la restricción 1 es del tipo '≤' se agrega la variable de holgura X4.
 Como la restricción 2 es del tipo '≤' se agrega la variable de holgura X5.
 Como la restricción 3 es del tipo '≤' se agrega la variable de holgura X6.
 Como la restricción 4 es del tipo '≤' se agrega la variable de holgura X7.
 Como la restricción 5 es del tipo '≤' se agrega la variable de holgura X8.
Tabla 1 3 4 8 0 0 0 0 0
Base Cb P0 P1 P2 P3 P4 P5 P6 P7 P8
P4 0 8 4 1 3 1 0 0 0 0
P5 0 4 6 2 1 0 1 0 0 0
P6 0 8 1 3 6 0 0 1 0 0
P7 0 12 3 2 8 0 0 0 1 0
P8 0 10 4 6 1 0 0 0 0 1
Z 0 -3 -4 -8 0 0 0 0 0
Tabla 2 3 4 8 0 0 0 0 0
Base Cb P0 P1 P2 P3 P4 P5 P6 P7 P8
P4 0 4 3.5 -0.5 0 1 0 -0.5 0 0
P5 0 2.67 5.83 1.5 0 0 1 -0.167 0 0
P3 8 1.33 0.17 0.5 1 0 0 0.167 0 0
P7 0 1.33 1.67 -2 0 0 0 -1.33 1 0
P8 0 8.67 3.83 5.5 0 0 0 -0.17 0 1
Z 10.67 -1.67 0 0 0 0 1.33 0 0

3. Tabla 3 3 4 8 0 0 0 0 0
Base Cb P0 P1 P2 P3 P4 P5 P6 P7 P8
P4 0 2.4 0 -1.4 0 1 -0.6 -0.4 0 0
P1 3
0.45714285
714286
1
0.257142
8
0 0
0.171428
57
-
0.028571428
571429
0 0
P3 8
1.25714285
71429
0
0.457142
857
1 0
-
0.028571
4285714
29
0.171428571
42857
0 0
P7 0
0.57142857
142857
0
-
2.428571
4
0 0
-
0.285714
2857142
9
-
1.285714285
7143
1 0
P8 0
6.91428571
42857
0
4.514285
7
0 0
-
0.657142
8571428
6
-
0.057142857
142857
0 1
Z
11.4285714
28571
0
0.428571
4285714
3
0 0
0.285714
2857142
9
1.285714285
7143
0 0
La solución óptima es
Z = 11.428571428571
X1 = 0.45714285714286
X2 = 0
X3 = 1.2571428571429