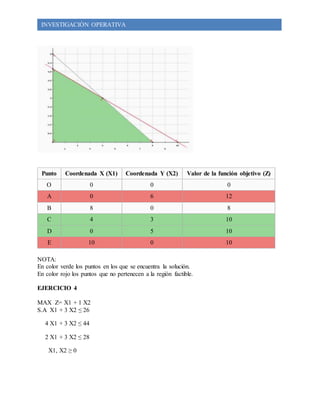
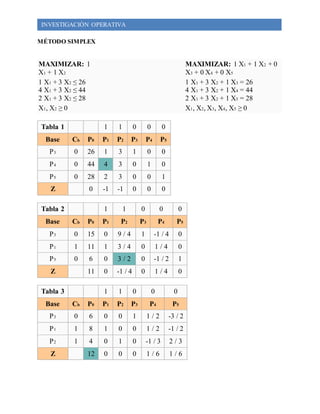
Este documento presenta cuatro ejercicios de programación lineal resueltos mediante el método simplex y gráfico. El primer ejercicio maximiza una función objetivo sujeta a restricciones, obteniendo una solución óptima de Z=5. El segundo ejercicio maximiza las utilidades de una empresa maderera usando el método simplex. El tercer ejercicio tiene infinitas soluciones óptimas. El cuarto ejercicio maximiza otra función objetivo con restricciones, dando como solución Z=12 y valores óptimos de X1

1. INVESTIGACIÒN OPERATIVA

2. INVESTIGACIÒN OPERATIVA
NOMBRE JESSICA PÈREZ
FECHA: 29 DE OCTUBRE DE 2014
EJERCICIO 1
Maximizar
Z = 2x1+ x2
s. r.
3x1+ x2 ≤6
x1- x2 ≤2
x2≤3
x1≥0 , x2≥0
MAXIMIZAR: 2 X1 +
1 X2
MAXIMIZAR: 2 X1 + 1 X2 + 0
h1 + 0 h2 + 0 h3
3 X1 + 1 X2 ≤ 6
1 X1 -1 X2 ≤ 2
0 X1 + 1 X2 ≤ 3
3 X1 + 1 X2 + 1 X3 = 6
1 X1 -1 X2 + 1 X4 = 2
0 X1 + 1 X2 + 1 X5 = 3
X1, X2 ≥ 0 X1, X2, H1, H2, H3 ≥ 0
Tabla 1 2 1 0 0 0
Base Cb P0 P1 P2 P3 P4 P5
P3 0 6 3 1 1 0 0
P4 0 2 1 -1 0 1 0
P5 0 3 0 1 0 0 1
Z 0 -2 -1 0 0 0
Tabla 2 2 1 0 0 0
Base Cb P0 P1 P2 P3 P4 P5
P3 0 0 0 4 1 -3 0

3. INVESTIGACIÒN OPERATIVA
P1 2 2 1 -1 0 1 0
P5 0 3 0 1 0 0 1
Z 4 0 -3 0 2 0
Tabla 3 2 1 0 0 0
Base Cb P0 P1 P2 P3 P4 P5
P2 1 0 0 1 1 / 4 -3 / 4 0
P1 2 2 1 0 1 / 4 1 / 4 0
P5 0 3 0 0 -1 / 4 3 / 4 1
Z 4 0 0 3 / 4 -1 / 4 0
Tabla 4 2 1 0 0 0
Base Cb P0 P1 P2 P3 P4 P5
P2 1 3 0 1 0 0 1
P1 2 1 1 0 1 / 3 0 -1 / 3
P4 0 4 0 0 -1 / 3 1 4 / 3
Z 5 0 0 2 / 3 0 1 / 3
La solución óptima es Z = 5
X1 = 1
X2 = 3
MÉTODO GRÁFICO:
MAXIMIZAR: 2 X1 + 1 X2
3 X1 + 1 X2 ≤ 6
1 X1 -1 X2 ≤ 2
0 X1 + 1 X2 ≤ 3
X1, X2 ≥ 0

4. INVESTIGACIÒN OPERATIVA
Punto
Coordenada X
(X1)
Coordenada Y
(X2)
Valor de la función objetivo
(Z)
O 0 0 0
A 0 6 6
B 2 0 4
C 1 3 5
D 5 3 13
E 0 3 3
NOTA:
En color verde los puntos en los que se encuentra la solución.
En color rojo los puntos que no pertenecen a la región factible.

5. INVESTIGACIÒN OPERATIVA
EJERCICIO 2
2. La empresa el SAMÁN Ltda. Dedicada a la fabricación de muebles, ha ampliado su
producción en dos líneas más. Por lo tanto actualmente fabrica mesas, sillas, camas y
bibliotecas. Cada mesa requiere de 2 piezas rectangulares de 8 pines, y 2 piezas
cuadradas de 4 pines. Cada silla requiere de 1 pieza rectangular de 8 pines y 2 piezas
cuadradas de 4 pines, cada cama requiere de 1 pieza rectangular de 8 pines, 1 cuadrada
de 4 pines y 2 bases trapezoidales de 2 pines y finalmente cada biblioteca requiere de 2
piezas rectangulares de 8 pines, 2 bases trapezoidales de 2 pines y 4 piezas rectangulares
de 2 pines. Cada mesa cuesta producirla $10000 y se vende en $ 30000, cada silla cuesta
producirla $ 8000 y se vende en $ 28000, cada cama cuesta producirla $ 20000 y se
vende en $ 40000, cada biblioteca cuesta producirla $ 40000 y se vende en $ 60000. El
objetivo de la fábrica es maximizar las utilidades.
MÉTODO SIMPLEX

6. INVESTIGACIÒN OPERATIVA
MAXIMIZAR: 20000
X1 + 20000 X2 + 20000
X3 + 20000 X4
MAXIMIZAR: 20000 X1 +
20000 X2 + 20000 X3 +
20000 X4 + 0 X5 + 0 X6 + 0
X7 + 0 X8
2 X1 + 1 X2 + 1 X3 + 2
X4 ≤ 24
2 X1 + 2 X2 + 1 X3 + 0
X4 ≤ 20
0 X1 + 0 X2 + 2 X3 + 2
X4 ≤ 20
0 X1 + 0 X2 + 0 X3 + 4
X4 ≤ 16
2 X1 + 1 X2 + 1 X3 + 2 X4 + 1
X5 = 24
2 X1 + 2 X2 + 1 X3 + 1 X6 =
20
0 X1 + 2 X3 + 2 X4 + 1 X7 =
20
0 X1 + 4 X4 + 1 X8 = 16
X1, X2, X3, X4 ≥ 0
X1, X2, X3, X4, X5, X6, X7,
X8 ≥ 0
Tabla 1 20000 20000 20000 20000 0 0 0 0
Base Cb P0 P1 P2 P3 P4 P5 P6 P7 P8
P5 0 24 2 1 1 2 1 0 0 0
P6 0 20 2 2 1 0 0 1 0 0
P7 0 20 0 0 2 2 0 0 1 0
P8 0 16 0 0 0 4 0 0 0 1
Z 0 -20000 -20000 -20000 -20000 0 0 0 0
Tabla
2
20000 20000 20000 20000 0 0 0 0
Base Cb P0 P1 P2 P3 P4 P5 P6 P7 P8
P5 0 4 0 -1 0 2 1 -1 0 0
P1 20000 10 1 1 0.5 0 0 0.5 0 0
P7 0 20 0 0 2 2 0 0 1 0

7. INVESTIGACIÒN OPERATIVA
P8 0 16 0 0 0 4 0 0 0 1
Z 200000 0 0 -10000 -20000 0 10000 0 0
Tabla 3 20000 20000 20000 20000 0 0 0 0
Base Cb P0 P1 P2 P3 P4 P5 P6 P7 P8
P5 0 4 0 0 0 1 0 0 0 0.25
P1 20000 6 1 0 0.5 0 1 -0.5 0 -0.5
P7 0 12 0 0 2 0 0 0 1 -0.5
P2 20000 4 0 1 0 0 -1 1 0 0.5
Z 200000 0 0
-
10000
-
20000
0 10000 0 0
Tabla
4
20000 20000 20000 20000 0 0 0 0
Base Cb P0 P1 P2 P3 P4 P5 P6 P7 P8
P4 20000 4 0 0 0 1 0 0 0 0.25
P1 20000 6 1 0 0.5 0 1 -0.5 0 -0.5
P7 0 12 0 0 2 0 0 0 1 -0.5
P2 20000 4 0 1 0 0 -1 1 0 0.5
Z 280000 0 0
-
10000
0 0 10000 0 5000
Tabla
5
20000 20000 20000 20000 0 0 0 0
Base Cb P0 P1 P2 P3 P4 P5 P6 P7 P8
P4 20000 4 0 0 0 1 0 0 0 1 / 4
P1 20000 3 1 0 0 0 1 -1 / 2
-1 /
4
-3 / 8

8. INVESTIGACIÒN OPERATIVA
P3 20000 6 0 0 1 0 0 0 1 / 2 -1 / 4
P2 20000 4 0 1 0 0 -1 1 0 1 / 2
Z 340000 0 0 0 0 0 10000 5000 2500
Hay infinitos valores de X1, X2, X3, X4 para el valor óptimo Z = 340000 , los cuales están
contenidos en la región del espacio 20000 X1 + 20000 X2 + 20000 X3 + 20000 X4 = 340000
que cumple las restricciones del problema.
Una de ellas es:
X1 = 3
X2 = 4
X3 = 6
X4 = 4
EJERCICIO 3
Maximizar:
Sujeto a:
MÉTODO SIMPLEX
MAXIMIZAR: 1 X1 +
2 X2
MAXIMIZAR: 1 X1 + 2 X2 + 0
H1 + 0 H2

9. INVESTIGACIÒN OPERATIVA
0,75 X1 + 1 X2 ≤ 6
0,5 X1 + 1 X2 ≤ 5
0.75 X1 + 1 X2 + 1 X3 = 6
0.5 X1 + 1 X2 + 1 X4 = 5
X1, X2 ≥ 0
X1, X2, H1, H2 ≥ 0
Tabla 1 1 2 0 0
Base Cb P0 P1 P2 P3 P4
P3 0 6 0.75 1 1 0
P4 0 5 0.5 1 0 1
Z 0 -1 -2 0 0
Tabla 2 1 2 0 0
Base Cb P0 P1 P2 P3 P4
P3 0 1 0.25 0 1 -1
P2 2 5 0.5 1 0 1
Z 10 0 0 0 2
Hay infinitos valores de X1, X2 para el valor óptimo Z = 10 , los cuales están contenidos en el
segmento de la recta 1 X1 + 2 X2 = 10 que cumple las restricciones del problema.
Una de ellas es:
X1 = 0
X2 = 5
MÉTODO GRAFICO
MAXIMIZAR: 1 X1 + 2 X2
0.75 X1 + 1 X2 ≤ 6
0.5 X1 + 1 X2 ≤ 5
X1, X2 ≥ 0
El problema tiene infinitas soluciones.

10. INVESTIGACIÒN OPERATIVA
Punto Coordenada X (X1) Coordenada Y (X2) Valor de la función objetivo (Z)
O 0 0 0
A 0 6 12
B 8 0 8
C 4 3 10
D 0 5 10
E 10 0 10
NOTA:
En color verde los puntos en los que se encuentra la solución.
En color rojo los puntos que no pertenecen a la región factible.
EJERCICIO 4
MAX Z= X1 + 1 X2
S.A X1 + 3 X2 ≤ 26
4 X1 + 3 X2 ≤ 44
2 X1 + 3 X2 ≤ 28
X1, X2 ≥ 0

11. INVESTIGACIÒN OPERATIVA
MÉTODO SIMPLEX
MAXIMIZAR: 1
X1 + 1 X2
MAXIMIZAR: 1 X1 + 1 X2 + 0
X3 + 0 X4 + 0 X5
1 X1 + 3 X2 ≤ 26
4 X1 + 3 X2 ≤ 44
2 X1 + 3 X2 ≤ 28
1 X1 + 3 X2 + 1 X3 = 26
4 X1 + 3 X2 + 1 X4 = 44
2 X1 + 3 X2 + 1 X5 = 28
X1, X2 ≥ 0 X1, X2, X3, X4, X5 ≥ 0
Tabla 1 1 1 0 0 0
Base Cb P0 P1 P2 P3 P4 P5
P3 0 26 1 3 1 0 0
P4 0 44 4 3 0 1 0
P5 0 28 2 3 0 0 1
Z 0 -1 -1 0 0 0
Tabla 2 1 1 0 0 0
Base Cb P0 P1 P2 P3 P4 P5
P3 0 15 0 9 / 4 1 -1 / 4 0
P1 1 11 1 3 / 4 0 1 / 4 0
P5 0 6 0 3 / 2 0 -1 / 2 1
Z 11 0 -1 / 4 0 1 / 4 0
Tabla 3 1 1 0 0 0
Base Cb P0 P1 P2 P3 P4 P5
P3 0 6 0 0 1 1 / 2 -3 / 2
P1 1 8 1 0 0 1 / 2 -1 / 2
P2 1 4 0 1 0 -1 / 3 2 / 3
Z 12 0 0 0 1 / 6 1 / 6

12. INVESTIGACIÒN OPERATIVA
La solución óptima es Z = 12
X1 = 8
X2 = 4
MÉTODO GRAFICO
MAXIMIZAR: 1 X1 + 1 X21 X1 + 3 X2 ≤ 26
4 X1 + 3 X2 ≤ 44
2 X1 + 3 X2 ≤ 28
X1, X2 ≥ 0
Punto Coordenada X (X1) Coordenada Y (X2) Valor de la función objetivo (Z)
O 0 0 0
A 0 26 / 3 26 / 3
B 26 0 26
C 6 20 / 3 38 / 3
D 2 8 10
E 0 44 / 3 44 / 3
F 11 0 11

13. INVESTIGACIÒN OPERATIVA
G 8 4 12
H 0 28 / 3 28 / 3
I 14 0 14
NOTA:
En color verde los puntos en los que se encuentra la solución.
En color rojo los puntos que no pertenecen a la región factible.