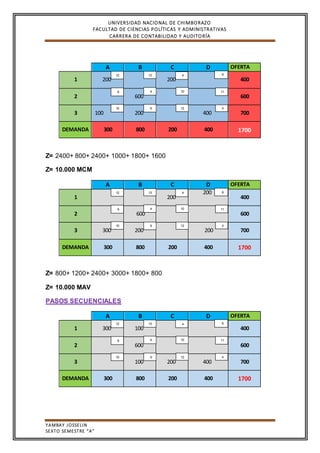
El documento presenta ejemplos resueltos del método de la esquina del noroeste, método de aproximación de Vogel, método de asignación y método de pasos secuenciales para resolver problemas de transporte. Incluye tablas con oferta y demanda de diferentes orígenes y destinos, y los cálculos de las funciones objetivo para cada método.