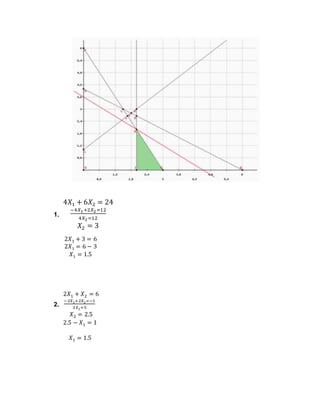
El documento presenta tres problemas de programación lineal. El primer problema involucra una fábrica de pintura que debe determinar la producción óptima de pintura interior y exterior para maximizar las utilidades, sujeto a restricciones en los insumos. El segundo problema busca minimizar una función objetivo sujeto a restricciones. El tercer problema busca maximizar y minimizar una función objetivo sujeta a restricciones. Se resuelven los tres problemas gráficamente encontrando los valores óptimos, restricciones activas e inactivas, y holguras o excedentes

1. UNIVERSIDAD NACIONAL DE CHIMBORAZO
FACULTAD DE CIENCIAS POLITICAS Y ADMINISTRATIVAS
RIOBAMBA ECUADOR
ESCUELA: CONTABILIDAD Y AUDITORÍA DOCENTE: Doctor MarlonVillaVillaMs.C.
DISCENTE: YAMBAY JOSSSELIN FECHA: 2014-10-22 SEMESTRE: 5º “A”
TEMA: MÉTODO GRÁFICO
1. INDICACIONESGENERALES
 La presente Pruebaserá calificadasobre4 puntos
 Cadaproblemaresuelto vale un puntoexcepto el tercero que vale 2 puntos
 El tiempo estimadoparala prueba es de 50 minutos
2. C U E S T I O N A R I O.
Hallar el valor óptimo,la soluciónóptima,las restriccionesactivas, las restriccionesinactivas,la
holgura o el excedente de lossiguientesproblemas.
1) Una fábrica de pinturaproduce pinturas para interiores y exteriores, a partir de dos materias
primasM1 y M2. Por cada toneladade pinturapara interioresse requiere4toneladas de M1 y
2 toneladasde M2. Y para cada toneladade pinturaparaexteriores se requiere 6toneladasde
M1 y una de M2. Se dispone de 24 toneladas de M1 y 6 de M2 diariamente. La utilidad que
arroga una toneladade pinturapara exterioresesde $ 5 000 y de una toneladaparainteriores
esde $ 4 000. La demandamáximadiariade pinturaparainterioresesde 2 toneladas.Además
la demandadiariade pinturapara interioresnopuedeexceder a la de pintura para exteriores
por más de una tonelada.Lacompañía quiere determinar la mezcla de producción óptima de
pinturas para interiores y exteriores que maximice las utilidades diarias y satisfaga las
limitaciones.
2) Min Z= 3F + 4G
s.a. F + G ≥ 8
2F + G ≥ 12
G ≥ 2
F ≤ 10
F , G ≥ 0
3) Para el siguiente problemade programación lineal:
Z = 3X1 – 5X2
Restricciones:5X1 – 4X2 ≥ -20
X1 ≤ 8

2. X2 ≤ 10
X2 ≥ 3
5X1 + 4X2 ≥ 20
Xj ≥0 ; j =1,2
a) Cuál esel valor de X1 y X2 que maximizala funciónobjetivoZ.
b) Cuál esel valor de X1 y X2 que minimizala funciónobjetivoZ.
Maximizar: Z= 4000X1+ 5000X2
1. 4𝑋1 + 6𝑋2 ≤ 24
4𝑋1 + 6𝑋2 = 24
2. 2𝑋1 + 𝑋2 ≤ 6
2𝑋1 + 𝑋2 = 6
3. 𝑋1 ≥ 2
4. 𝑋2 − 𝑋1 ≤ 1
𝑋1, 𝑋2 ≤ 0
X1 X2
0 4
6 0
X1 X2
0 6
3 0
1

3. 1.
4𝑋1 + 6𝑋2 = 24
−4𝑋1+2𝑋2=12
4𝑋2=12
𝑋2 = 3
2𝑋1 + 3 = 6
2𝑋1 = 6 − 3
𝑋1 = 1.5
2.
2𝑋1 + 𝑋2 = 6
−2𝑋1+2𝑋2=−1
3𝑋2=5
𝑋2 = 2.5
2.5 − 𝑋1 = 1
𝑋1 = 1.5

4. HOLGURAS O EXCEDENTES
1.
𝑿 𝟏 − 𝑿 𝟐 + 𝑯 ≤ 𝟏
𝟑 − 𝟏. 𝟓 + 𝑯 ≤ 𝟏
𝑯 = 𝟎. 𝟓
MINIMIZAR: Z= 3F+ 4G
1. 𝐹 + 𝐺 ≥ 8
2. 2𝐹 + 𝐺 ≥ 12
3. 𝐺 ≥ 2
4. 𝐹 ≤ 10
𝐹, 𝐺 ≥ 0
VALORES ÓPTIMOS
Z 21000
X1 1.5
X2 3
r.a 1,2
r.i 3,4
F G
0 8
8 0
F G
0 12
6 0
HOLGURA
2

5. 𝑭+𝑮=𝟖
𝟐𝑭+𝑮=𝟏𝟐 (−𝟏)
−𝑭= −𝟒
𝑭=𝟒
𝑭 + 𝑮 = 𝟖
𝟒(𝟏)+ 𝑮 = 𝟖
𝟒 + 𝑮 = 𝟖
𝑮 = 𝟖 − 𝟒
𝑮 = 𝟒
𝒁 = 𝟑𝑭 + 𝟒𝑮
𝒁 = 𝟑( 𝟒)+ 𝟒(𝟒)
𝒁 = 𝟐𝟖
VALORES ÓPTIMOS
Z 28
F 4
G 4
R.A. 1,2
R.I. 3,4

6. HOLGURAS O EXCEDENTES
2.
𝑭 + 𝑮 + 𝑯𝟏 = 𝟖
𝟒 + 𝟒 + 𝑯𝟏 = 𝟖
𝑯𝟏 = 𝟖 − 𝟖
𝑯𝟏 = 𝟎
3.
𝟐𝑭 + 𝑮 + 𝑯𝟐 = 𝟏𝟐
𝟐( 𝟒) + 𝟒 + 𝑯𝟐 = 𝟏𝟐
𝑯𝟐 = 𝟏𝟐− 𝟏𝟐
𝑯𝟐 = 𝟎
4.
𝑮 − 𝑯𝟑 = 𝟐
𝟒 − 𝑯𝟑 = 𝟐
−𝑯𝟑 = 𝟐 − 𝟒
−𝑯𝟑 = −𝟐
𝑯𝟑 = 𝟐
(excedente)
5.
𝑭 + 𝑯𝟒 = 𝟏𝟎
𝟒 + 𝑯𝟒 = 𝟏𝟎
𝑯𝟒 = 𝟏𝟎 − 𝟒
𝑯𝟒 = 𝟔
(holgura)
FUNCIÓNOBJETIVO: MAXIMIZAR Z = 3X1 – 5X2
Restricciones:
5X1 – 4X2 ≥ -20
X1 ≤ 8
X2 ≤ 1
X2 ≥ 3
5X1 + 4X2 ≥ 20
Xj ≥0 ; j =1,2
1) 5X1 – 4X2 = -20
x y
0
-4
5
0
2) X1 = 8
3) X2 = 10
4) X2 = 3
5) 5X1 + 4X2 =20
x y
0
4
5
0
3
a)

7. La soluciónóptimaes
z=9
X1= 8
X2=3

8. El problemanoestáacotado perocomo se trata de unproblemade minimizaciónesposible
encontraruna solución.
1) 5X1 – 4X2 = -20
x y
0
-4
5
0
2) X1 = 8
3) X2 = 10
4) X2 = 3
5) 5X1 + 4X2 =20
x y
0
4
5
0
MINIMIZAR: 3 X1 -5 X2
-5 X1 + 4 X2 ≥ 20
1 X1 + 0 X2 ≥ 8
0 X1 + 1 X2 ≥ 10
0 X1 + 1 X2 ≥ 3
5 X1 + 4 X2 ≥ 20
X1, X2 ≥ 0
b)

9. Punto
Coordenada X
(X1)
Coordenada Y
(X2)
Valor de la función objetivo
(Z)
O 0 0 0
A 0 5 -25
B 8 15 -51
C 4 10 -38
D 8 0 24
E 8 10 -26
F 8 3 9
G 0 10 -50
H 0 3 -15
I 1.6 3 -10.2
J 4 0 12
NOTA:
En color verde los puntos en los que se encuentra la solución.
En color rojo los puntos que no pertenecen a la región factible