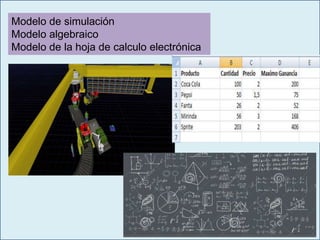
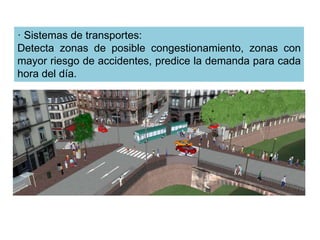
El documento aborda la enseñanza de la ciencia mediante la modelación y simulación, enfatizando en la importancia de los modelos y sus tipos, así como los beneficios de la simulación en el aprendizaje. Se discuten las características, ejemplos y aplicaciones de diferentes modelos, incluyendo modelos físicos, matemáticos, estocásticos y gráficos. Además, se explora la simulación en contextos educativos y en diversos sistemas naturales y humanos, resaltando su papel en el desarrollo de habilidades y comprensión del estudiante.

1. ESCUELA NORMAL SUPERIOR
DEL SUR DE TAMAULIPAS
LAS ENSEÑANZAS DE LA CIENCIA CON TECNOLOGÍA
LA MODELACIÓN Y LA SIMULACIÓN EN CIENCIAS.
NORMALISTA: DIANA VIRGINIA CASTRO SANTIAGO
SEXTO SEMESTRE ESPECIALIDAD DE FÍSICA
ING. JOSÉ ALEJANDRO SALINAS ORTA.
Deana_vicki96@hotmail.com
02 DE SEPTIEMBRE DEL 2017 TAMPICO TAMAULIPAS

2. INTRODUCCIÓN
Es importante que los estudiantes analicen
detalladamente los diferentes tipos de modelos .
Por medio de esta presentación se explicará en que
consiste cada modelo, además podrán analizar las
características y algunos ejemplos para
representarlos.
Al final de la información brindada habrá un test
para reforzar el contenido analizado y una practica
por medio de una simulación.

3. ÍNDICE
Definición de modelo
Tipos de modelo
Características
Ejemplos
 Definición de simulación
Tipos de simulación
características
Ejemplos
A practicar
Referencias.

4. Un Modelo muestra características únicas que
resaltan una idea, esta puede ser o no seguida
por quienes la perciben.
Definición de
modeloUn Modelo es un prototipo que sirve de referencia y
ejemplo para todos los que diseñan y confeccionan.

5. Este tipo de modelo se identifica por la
representación de un elemento determinado,
proporcionando la oportunidad de exponerlo.
Se hace el prototipo con el propósito de estudiar
detalladamente el comportamiento de la
estructura, o parte de ella, bajo ciertas
circunstancias pre-establecidas de flujo.
La escala puede variar
de acuerdo al modelo
realizado.
MODELOS FÍSICOS:

6. Ejemplos:
Modelo de un aeroplano
Modelo de una casa
Modelo de una ciudad.

7. Tienen como finalidad la representación de distintos
fenómenos, o los vínculos existentes entre ellos, por
medio de una fórmula de carácter matemático.
Se pueden clasificar en:
MODELOS MATEMÁTICOS:
DETERMINISTAS NUMERICOS
ESTOCÁSTICO

8. Cuentan con los datos empleados; que las
fórmulas utilizadas son de tal exactitud, que
lograrán obtener un resultado preciso.
Por ejemplo, la Ley de gravitación formulada por
Newton.
MODELOS DETERMINISTAS:
La palabra determinista significa que
todos los aspectos del modelo ya se
conocen con certeza.
*A menudo ofrecen una aproximación
aceptable a la realidad.

9. Características
:
• Se utilizan técnicas de análisis de la
información .
• Interpreta los resultados.
• Utilizan hojas de calculo
• Solución de problemas.
• Utilización de formulas

11. MODELOS NUMÉRICOS:
Determina el conjunto de ecuaciones que
gobiernan el sistema que se estudia y del
cual se tienen observaciones metódicas.
El propósito es resolver las
ecuaciones de un modelo
matemático no de forma
analítica sino numérica.

12. PROCESO:
• Escoger el conjunto de observaciones (Datos)
• Definir el modelo conceptual (simplificaciones,
aproximaciones, hipótesis)
• Encontrar un modelo físico-matemático, un conjunto de
ecuaciones que represente al modelo conceptual.
• Encontrar un método de resolución numérica de dichas
ecuaciones.
• Encontrar la resolución del modelo matemático
• Capaz de explicar las observaciones.
• Interpretar los resultados

13. Ejemplos:

14. También conocidos como modelos probabilísticos, algún
elementó no se conoce con anticipación, incorporando
así la incertidumbre. Esta clase de modelo no se conocen
los datos con exactitud, de manera que se observa un
cierto grado de incertidumbre. Como consecuencia, el
resultado obtenido representara una probabilidad y no
una certeza total.
MODELOS ESTOCÁSTICO:
incertidumbre:
Falta de seguridad, de
confianza o de certeza
sobre algo, especialmente
cuando crea inquietud.
sólo se dispone de información recogida
durante periodos de observación breves.

15. Ejemplos:
filas de espera, administración de proyectos y pronóstico.

16. Incluyen la figuración
de datos numéricos por
medio de técnicas
gráficas determinadas,
tales como símbolos o
vectores.
MODELOS GRÁFICOS:

17. Características:
• Datos
• Análisis e Interpretación de la información
• Organización.
Tipos de gráficos:
*Columnas
*Con, cilindro y pirámide
*Barras
*Líneas
*Área
*Burbujas
*Circular
*Anillos

18. Es una representación material de un objeto
o proceso para comprender su origen,
formación o funcionamiento.
Es usado en ciencia e ingeniería para
validar las hipótesis y aproximaciones
mediante el calculo numérico.
.
Modelos análogos:

19. Características:
• Lenguaje
• Comprensión
• Nuevos conceptos
• Creatividad
• Generar nuevas ideas
• Razonamiento
• Resolución de
problemas.
Ejemplos:
• Mapa de carreteras
• Velocímetro
• Grafica de pastel.

20. Modelo simbólico
Emplea las matemáticas para representar las
relaciones entre los datos de interés. Requiere de
datos que sean posibles de expresarlos en forma
numérica.
La mayoría de las ecuaciones contenidas en un
modelo simbólico son simples relaciones de
contabilidad o definiciones físicas.

21. Modelo de simulación
Modelo algebraico
Modelo de la hoja de calculo electrónica

22. SIMULACIÓ
N

23. DEFINICIÓN DE
SIMULACIÓN

24. En el área de las ciencias son de gran ayuda ya que los
estudiantes relacionan conceptos (el choque de
moléculas) y también ayuda en el sentido de los
recursos como la simulación de un laboratorio entero.
Alan Turing usó el término
"simulación" para referirse a lo que
pasa cuando una computadora
digital describe las transiciones de
estado, las entradas y salidas de
una máquina.

25. Es un intento de modelar situaciones de la vida real por
medio de un programa de computadora, lo que requiere
ser estudiado para ver cómo es que trabaja el sistema.
• Sistemas naturales en física, química y biología.
• sistemas humanos como la economía y las ciencias
sociales.
Simulación por computadora

26. Categorías de la Simulación
1.Simulación de ‘’Vida’’
Es cuando las personas
reales usan el equipo
simulando el mundo real.
2.Simulación "Virtual", es cuando
las personas reales usan equipo
simulando mundos o ambientes
virtuales.

27. 3. Simulación "Constructiva", es cuando personas
simuladas, usan equipo simulado, en ambientes
simulados.

28. · Procesos de manufacturas:
Ayuda a distribuir el personal y a la
fabricación.
· Sistemas públicos:
Predice la demanda de energía durante
las diferentes épocas del año, anticipa el
comportamiento del clima, predice la
forma de propagación de enfermedades.
Áreas en las que se puede
utilizar la simulación:

29. · Sistemas de transportes:
Detecta zonas de posible congestionamiento, zonas con
mayor riesgo de accidentes, predice la demanda para cada
hora del día.

30. · Construcción de desastres naturales.
Predice el efecto de los vientos y
temblores sobre la estabilidad de los
edificios, provee información sobre las
condiciones ambientales en el interior de
los mismos, detecta las partes de las
estructuras que deben ser reforzadas.

31. Simulación en la educación
Consiste en situar al alumno en un contexto que imite
algún aspecto de la realidad y en establecer en ese
ambiente situaciones o problemáticas.
La simulación en la educación permiten al aprendiz :
• Observar
• Solucionar problemas
• Jugar
• Escuchar la información mediante viñetas narrativas
animadas (caricaturas).
• Llegar al conocimiento por medio del trabajo
exploratorio
• Desarrollo de habilidades.

32. • Su papel motivacional: permiten la
representación de fenómenos de estudio
que potencialmente captan la atención e
interés del estudiante.
• Su papel facilitador del aprendizaje: el
estudiante interactúa, favoreciendo el
descubrimiento y la comprensión del
fenómeno o sistema.
• Su papel reforzador, ayuda al aprendiz a
aplicar los conocimientos adquiridos y, por
ende, a la generalización del conocimiento.
Un simulador debe contar con las
siguientes características

33. Investigación de operaciones en la ciencia administrativa: construcción de modelos para
la toma de decisiones con hojas de cálculo electrónicas.
Gary D. Eppen
Pearson Educación, 2000 - 792 páginas
Modelado y Simulación Computacional de la Evacuación en caso de Emergencia en
Túneles Ferroviarios
Daniel Alvear
625 páginas
http://www.miliarium.com/Proyectos/Nitratos/Modelos/modelos/TiposModelos.asp
http://cinthyaraquelfiallos.blogspot.mx/2012/04/simuladores.html
https://es.wikipedia.org/wiki/Simulaci%C3%B3n
http://www.fca.unl.edu.ar/agromatica/Docs/07-ModelosAgronom.PDF
https://es.wikipedia.org/wiki/Simulador