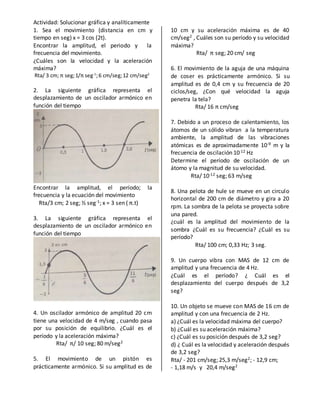
Este documento presenta problemas resueltos sobre movimiento circular uniforme y movimiento armónico simple. En la primera sección se explican conceptos como velocidad angular, velocidad lineal y aceleración centrípeta, y se resuelven 10 problemas que involucran estas cantidades para objetos que se mueven en círculo. La segunda sección explica elementos del movimiento armónico como amplitud, período y frecuencia, y resuelve 10 problemas que calculan estas cantidades y la posición, velocidad y aceleración para osciladores armónicos.

1. TEMA: Movimiento Circular Uniforme P / I 31 / III
11 0
- 01 / 02 2017
PROPÓSITO: Solucionar problemas propuestos delMCUA
“No se trata de conocer más; si no de ignorar menos. “ J.FLÓREZ
C I E N C I A S N A T U R A L E S A M B I E N T E Y S A L U D
Movimiento circular uniforme (m.c.u.): Es el generado por una partícula cuya
trayectoria es un circulo y el cual recorre con velocidad con constante.
Formulas:
Velocidad angular (𝜔): 𝜔 =
𝜃
𝑡
[ Rad / seg]
Velocidad lineal (Vl ): Vl =
2𝜋 𝑟
𝑇
ó Vl = ω. r
Periodo (T): T =
𝑡
𝑛
[seg]
Frecuencia (f): f =
𝑛
𝑡
[s-1 ó Hz] T . f = 1
Aceleración centrípeta (a c): ac =
𝑣2
𝑟
ó 𝑎 𝑐 = 𝜔2
. 𝑟
Ecuaciones cinemáticas:
𝜔𝑓 = 𝜔0 +𝛼. 𝑡; 𝜑 = 𝜔0 . 𝑡 +
1
2
𝛼. 𝑡2
; 𝜔𝑓
2
= 𝜔0
2
+2.𝛼. 𝜑
PROBLEMASPROPUESTOS:
1) Una ruedade 50 cm de radiogira a 180 r.p.m.
Calcula:a) El módulode la velocidadangularen
rad/s, b) El módulode lavelocidadlineal de su
borde,c) Sufrecuencia.
a) ω= 6 rad/s.B) v= 9.42 m/s , c) f= 3 Hz
2) Un CD-ROM, que tiene un radio de 6 cm, gira a
una velocidad de 2500 rpm. Calcula: a) El módulo
de la velocidad angular en rad/s, b) El módulo de
la velocidadlineal de suborde,c) Sufrecuencia.
a) ω= 83.3rad/s., b) v= 15.7 m/s, c) f= 41.66 Hz
3) Teniendo en cuenta que la Tierra gira
alrededor del Sol en 365.25 días y que el radio de
giro medio es de 1.5 1011 m, calcula (suponiendo
que se mueve en un movimiento circular
uniforme): a) El módulo de la velocidad angular en
rad/día, b) El módulo de la velocidad a que viaja
alrededor del Sol, c) El ángulo que recorrerá en 30
días. d) El módulo de la aceleración centrípeta
provocadapor el Sol.
a) ω= 0.0172 rad/día b) v= 29861m/s c)  = 0.516 rad =
29° 33' d) a= 5.9 10-3 m/s2
4) Calcular cuánto tiempo pasa entre dos
momentos en que Marte y Júpiter estén sobre el
mismo radio de sus órbitas (suponiendo que
ambos se mueven con un movimiento circular
uniforme). Periodos de sus órbitas alrededor del
Sol:Marte: 687.0 días Júpiter: 11.86 año
t= 816.6 días
5) Un piloto de avión bien entrenado aguanta
aceleraciones de hasta 8 veces la de la gravedad,
durante tiempos breves, sin perder el
conocimiento. Para un avión que vuela a 2300
km/h, ¿cuál será el radio de giro mínimo que
puede soportar?
r= 5200 m
6) Tenemos un cubo con agua atado al final de
una cuerda de 0.5 m y lo hacemos girar
verticalmente. Calcular: a) El módulo de la
velocidad lineal que debe adquirir para que la
aceleración centrípeta sea igual a 9.8 m/s2 . b) El
módulo de la velocidad angular que llevará en ese
caso
a) v =2.21 m/s b) ω = 4.42 rad/s = 0.70 vueltas/s
7) La Estación Espacial Internacional gira con
velocidad angular constante alrededor de la Tierra
cada 90 minutos en una órbita a 300 km de altura
sobre la superficie terrestre (por tanto, el radio de
la órbita es de 6670 km). a) Calcular la velocidad
angular , b) Calcular la velocidad lineal v y c)
¿Tiene aceleración? En caso afirmativo, indicar sus
características y, en caso negativo, explicar las
razonesde que no exista
a) ω = π/2700 rad/s b) v =7760 m/s.

2. 8) Una centrifugadora de 15 cm de radio gira a
700 r.p.m. calcula la velocidad a la que se
desprendende suborde lasgotasde agua.
v =11,0 m/s
9) Un aerogenerador cuyas aspas tienen 10 m de
radio gira dando una vuelta cada 3 segundos.
Calcula: a) Su velocidad angular. b) Su frecuencia
c) La velocidad lineal del borde del aspa. d) La
aceleracióncentrípetaenel centrodel aspa.
a) ω = 2π/3 rad/s ; b) f= Hz ; c) v = 20,9 m/s ;
d) ac = 87,4 m/s2
10) Un ventilador de 20 cm de diámetro gira a
120 r.p.m. Calcula: a) Su velocidad angular en
unidades S.I. b) La aceleración centrípeta en el
borde externodel aspa.
a)ω = 4π rad/s ; b) ac= 15,8 m/s2
Movimiento circular uniformemente acelerado
(m.c.u.a.)
11) Un CD-ROM de 6 cm de radio gira a una
velocidad de 2500 rpm. Si tarda en pararse 15 s,
calcula: a) El módulo de la aceleración angular. b)
Las vueltas que da antes de detenerse. c) El
módulode lavelocidadangularparat=10 s
a) = -5.55 rad/s2 b)  = 625 rad = 312.5 vueltas c)
= 27.77 rad/s
12) Un coche con unas ruedas de 30 cm de radio
acelera desde 0 hasta 100 km/h en 5 s. Calcular: a)
El módulo de la aceleración angular. b) Las vueltas
que daen ese tiempo. c) El módulo de la velocidad
angular para t=3 s, d) El módulo de la aceleración
tangencial y e) El módulo de la aceleración normal
para t= 5 s
a) = 18.52 rad/s2. b)  = 231.48 rad = 36.84 vueltas, c)
= 55.56 rad/s,d) aT= 5.55 m/s2, e) aN= 2572 m/s2
13) Una centrifugadora pasa de estar detenida a
girar a 450 r.p.m. en 15 s. Si el radio del tambor es
de 25 cm, calcular: a) El módulo de la aceleración
angular. b) Las vueltasque daenese tiempo.
c) El módulode lavelocidadangularparat=10 s,
d) El módulo de la aceleración tangencial y e) El
módulode laaceleraciónnormal parat=15 s
a) =  rad/s2, b)  = 112.5 rad = 56.25 vueltas; c)
= 10 rad/s,d) aT= 0.78 m/s2; e) aN= 555.2 m/s2
14) Una centrifugadoraesta girando a 1500 r.p.m.,
se desconecta y se detiene en 10 s. Calcular a) Su
aceleración angular  y b) Las vueltas que da
hasta detenerse.
a)  = -15.70 rad/s2 ; b)  =125 vueltas
15) Un disco que está girando a 2 vueltas/s, frena
y se detiene en 9 s. Calcular: a) Su aceleración
angular. b) Las vueltas que da hasta detenerse. c)
La velocidad del borde del disco para t=2 s si el
radiodel discoesde 15 cm.
a) =- 4π/9 rad/s2;b)  =9 vueltas;c) v =1,46 m/s
16) Dejamos caer un yo-yo y pasa de no girar a
hacerlo a 3 vueltas por segundo en los 2 segundos
que tarda en bajar. Calcula: a) Su aceleración
angular. b) Las vueltas que dará en los dos
segundos.
a) = 3  rad/s2;b)  = 6 rad = 3 vueltas.
17) Un automóvil con ruedas de 30 cm de
diámetro acelera de 0 a 30 m/s en 5 s. Calcula: a)
La aceleración angular de sus ruedas. b) La
aceleración lineal del coche y c) Las vueltas que da
la ruedamientras acelera.
a) = 20 rad/s2; b) a = 6 m/s2; c)  = 250 rad = 39,83
vueltas
Link:
http://www.elortegui.org/ciencia/datos/4ESO/eje
r/resueltos/Ejercicios%20movimiento%20circular
%20con%20solucion.pdf

3. TEMA: física de ondas P / II 17 / V
11 0
- 01 / 02 2017
PROPÓSITO: Solucionar problemas propuestos delmovimiento armónico simple.(M A S )
“No se trata de conocer más; si no de ignorar menos. “ J.FLÓREZ
C I E N C I A S N A T U R A L E S A M B I E N T E Y S A L U D
Elementos del M A S Gráficas
M A S: Es la proyección de un movimiento circular
uniforme sobre una línea recta. Eje X´- X.
Características Fórmulas
 Elongación(X):Distanciade un punto a
la posición de equilibrio(0)
 Amplitud:(A)Corresponde a la máxima
elongación.
 La fuerza que sostiene el MAS, es variable.
 La aceleración es máxima en los puntos
X`- X
 La velocidad es nula en los puntos X´-X
Posición: X = A.cos (ω.t + φ)
Velocidad: v= -ω.A sen(ω.t + φ)
Aceleración: a = -ω2. A cos(ω.t + φ)
Donde φ, representa la fase inicial del
movimiento.

4. Actividad: Solucionar gráfica y analíticamente
1. Sea el movimiento (distancia en cm y
tiempo en seg) x = 3 cos (2t).
Encontrar la amplitud, el periodo y la
frecuencia del movimiento.
¿Cuáles son la velocidad y la aceleración
máxima?
Rta/ 3 cm; π seg;1/π seg-1
;6 cm/seg;12 cm/seg2
2. La siguiente gráfica representa el
desplazamiento de un oscilador armónico en
función del tiempo
Encontrar la amplitud, el período; la
frecuencia y la ecuación del movimiento
Rta/3 cm; 2 seg; ½ seg-1; x = 3 sen ( π.t)
3. La siguiente gráfica representa el
desplazamiento de un oscilador armónico en
función del tiempo
4. Un oscilador armónico de amplitud 20 cm
tiene una velocidad de 4 m/seg , cuando pasa
por su posición de equilibrio. ¿Cuál es el
período y la aceleración máxima?
Rta/ π/ 10 seg; 80 m/seg2
5. El movimiento de un pistón es
prácticamente armónico. Si su amplitud es de
10 cm y su aceleración máxima es de 40
cm/seg2 , Cuáles son su período y su velocidad
máxima?
Rta/ π seg; 20 cm/ seg
6. El movimiento de la aguja de una máquina
de coser es prácticamente armónico. Si su
amplitud es de 0,4 cm y su frecuencia de 20
ciclos/seg, ¿Con qué velocidad la aguja
penetra la tela?
Rta/ 16 π cm/seg
7. Debido a un proceso de calentamiento, los
átomos de un sólido vibran a la temperatura
ambiente, la amplitud de las vibraciones
atómicas es de aproximadamente 10-9 m y la
frecuencia de oscilación 1012 Hz
Determine el período de oscilación de un
átomo y la magnitud de su velocidad.
Rta/ 10-12 seg; 63 m/seg
8. Una pelota de hule se mueve en un circulo
horizontal de 200 cm de diámetro y gira a 20
rpm. La sombra de la pelota se proyecta sobre
una pared.
¿cuál es la amplitud del movimiento de la
sombra ¿Cuál es su frecuencia? ¿Cuál es su
período?
Rta/ 100 cm; 0,33 Hz; 3 seg.
9. Un cuerpo vibra con MAS de 12 cm de
amplitud y una frecuencia de 4 Hz.
¿Cuál es el período? ¿ Cuál es el
desplazamiento del cuerpo después de 3,2
seg?
10. Un objeto se mueve con MAS de 16 cm de
amplitud y con una frecuencia de 2 Hz.
a) ¿Cuál es la velocidad máxima del cuerpo?
b) ¿Cuál es su aceleración máxima?
c) ¿Cuál es su posición después de 3,2 seg?
d) ¿ Cuál es la velocidad y aceleración después
de 3,2 seg?
Rta/ - 201 cm/seg; 25,3 m/seg2; - 12,9 cm;
- 1,18 m/s y 20,4 m/seg2