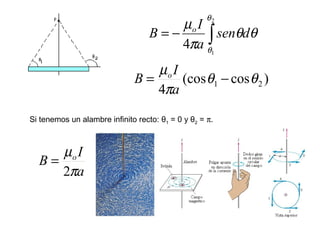
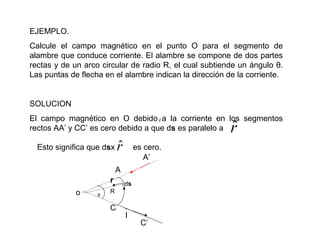
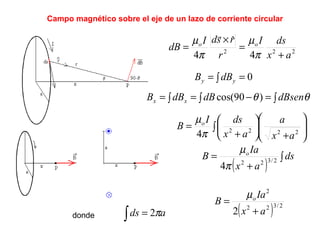
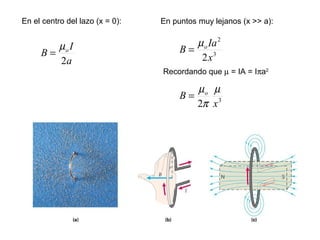
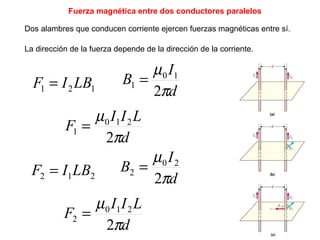
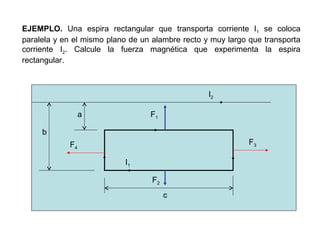
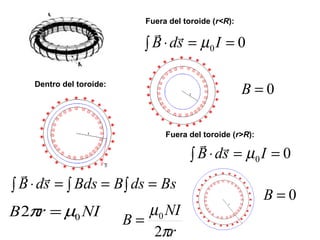
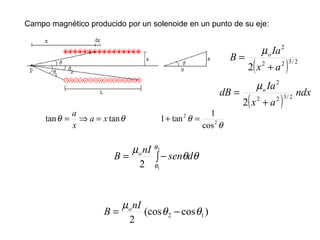
La ley de Biot-Savart describe las propiedades del campo magnético creado por una corriente eléctrica. El vector campo magnético dB es perpendicular a la dirección de la corriente y a la línea entre el elemento de corriente y el punto de observación. La magnitud de dB disminuye con la distancia al cuadrado y aumenta con la corriente y la longitud del elemento. El campo total se calcula integrando dB sobre toda la corriente.

2. La ley de Biot-Savart
Propiedades del campo magnético creado por una corriente eléctrica:
El vector dB es perpendicular tanto a ds (que es un vector que tiene
unidades de longitud y está en la dirección de la corriente) como del vector
unitario dirigido del elemento a P
La magnitud de dB es inversamente proporcional a
r2
, donde r es la distancia del elemento a P.
La magnitud de dB es proporcional a la corriente y a
la longitud ds del elemento.
La magnitud de dB es proporcional a senθ, donde θ
es el ángulo entre los vectores ds y .
rˆ
rˆ
2
ˆ
4 r
rsId
Bd o ×
=

π
µ µo: permeabilidad del espacio libre
A
mT
o
⋅
×= −7
104πµ

3. ∫
×
= 2
ˆ
4 r
rsdI
B o

π
µ
Campo magnético alrededor de un conductor recto delgado
kdxsenkrsdrsd ˆ)(ˆˆˆ θ=×=×

∫= 2
4 r
dxsenI
B o θ
π
µ
θ
θ
θ csca
sen
a
r
r
a
sen ==⇒=
θ
θ
θ cot
tan
tan a
a
x
x
a
−=−=⇒−=
θθdadx 2
csc=
θ
θ
θθ
π
µ
d
a
senaI
B o
∫= 22
2
csc
csc
4
θθ
π
µ
dsen
a
I
B o
∫−=
4

4. ∫−=
2
1
4
θ
θ
θθ
π
µ
dsen
a
I
B o
)cos(cos
4
21 θθ
π
µ
−=
a
I
B o
Si tenemos un alambre infinito recto: θ1 = 0 y θ2 = π.
a
I
B o
π
µ
2
=

5. EJEMPLO.
Calcule el campo magnético en el punto O para el segmento de
alambre que conduce corriente. El alambre se compone de dos partes
rectas y de un arco circular de radio R, el cual subtiende un ángulo θ.
Las puntas de flecha en el alambre indican la dirección de la corriente.
SOLUCION
El campo magnético en O debido a la corriente en los segmentos
rectos AA’ y CC’ es cero debido a que ds es paralelo a
rˆrˆ
rˆ
Esto significa que dsx rˆ es cero.
θo R
ds
r
I
A
A’
C
C’

6. 2
0
4 R
dsI
dB
π
µ
=
Puesto que I y R son constantes, se puede integrar esta ecuación sobre la
trayectoria curva AC.
θ
π
µ
π
θµ
π
µ
R
I
R
RI
ds
R
I
B
44
)(
4
0
2
0
2
0
=== ∫
θ se mide en radianes.

7. Campo magnético sobre el eje de un lazo de corriente circular
222
4
ˆ
4 ax
dsI
r
rsdI
dB oo
+
=
×
=
π
µ
π
µ

0=∫= yy dBB
∫=∫ −=∫= θθ dBsendBdBB xx )90cos(
∫ 





+






+
= 2222
4 ax
a
ax
dsI
B o
π
µ
( ) ∫
+
= ds
ax
Ia
B o
2/322
4π
µ
( ) 2/322
2
2 ax
Ia
B o
+
=
µ
∫ = ads π2donde

8. En el centro del lazo (x = 0):
a
I
B o
2
µ
=
En puntos muy lejanos (x >> a):
3
2
2x
Ia
B oµ
=
Recordando que µ = IA = Iπa2
3
2 x
B o µ
π
µ
=

9. Fuerza magnética entre dos conductores paralelos
Dos alambres que conducen corriente ejercen fuerzas magnéticas entre sí.
La dirección de la fuerza depende de la dirección de la corriente.
121 LBIF =
d
I
B
π
µ
2
10
1 =
d
LII
F
π
µ
2
210
1 =
212 LBIF =
d
I
B
π
µ
2
20
2 =
d
LII
F
π
µ
2
210
2 =

10. Conductores paralelos que conducen corriente en la misma dirección se
atraen entre sí, en tanto que conductores paralelos que conducen
corrientes en direcciones opuestas se repelen entre sí.
Si dos alambres paralelos a 1 m de distancia conducen la mismaSi dos alambres paralelos a 1 m de distancia conducen la misma
corriente y la fuerza por unidad de longitud de cada alambre es de 2corriente y la fuerza por unidad de longitud de cada alambre es de 2 ××
1010−−77
N/m, entonces la corriente se define comoN/m, entonces la corriente se define como 1 amperio (A)1 amperio (A)..
Si un conductor conduce una corriente estable de 1 A, entonces la
cantidad de carga que fluye por sección transversal del conductor en
1 s es 1 C.

11. EJEMPLO. Una espira rectangular que transporta corriente I1 se coloca
paralela y en el mismo plano de un alambre recto y muy largo que transporta
corriente I2. Calcule la fuerza magnética que experimenta la espira
rectangular.
a
b
c
F3F4
I2
I1
F1
F2

12. Los tramos horizontales de la espira y el alambre recto y muy largo forman
una configuración de alambres paralelos, en consecuencia la fuerza
resultante sobre la espira será:
F = F1 – F2






−=
−=
ba
cII
F
c
b
II
c
a
II
F
11
2
22
210
210210
π
µ
π
µ
π
µ
Las fuerzas F3 y F4 se cancelan.

13. Ley de Ampère
La integral de línea de B·ds alrededor de cualquier trayectoria cerrada es igual
a µ0I, donde I es la corriente estable total que pasa a través de cualquier
superficie delimitada por la trayectoria cerrada.
IsdB 0µ=∫ ⋅

BsdsBBdssdB =∫=∫=∫ ⋅

Ia
a
I
sdB 0
0
2
2
µπ
π
µ
==∫ ⋅


14. Fuera del toroide (r<R):
00 ==∫ ⋅ IsdB µ
0=BDentro del toroide:
BsdsBBdssdB =∫=∫=∫ ⋅

NIrB 02 µπ =
r
NI
B
π
µ
2
0
=
Fuera del toroide (r>R):
00 ==∫ ⋅ IsdB µ
0=B

15. Si suponemos que el solenoide
es muy largo comparado con el
radio de sus espiras, el campo
es aproximadamente uniforme y
paralelo al eje en el interior del
solenoide y es nulo fuera del
solenoide.
BxdlBBdlldB BCBC =∫=∫=∫ ⋅

NIBx 0µ=
x
NI
B 0µ
=
nIB 0µ=

16. Campo magnético producido por un solenoide en un punto de su eje:
( )
ndx
ax
Ia
dB o
2/322
2
2 +
=
µ
θθ tantan xa
x
a
=⇒=
θ
θ 2
2
cos
1
tan1 =+
∫ −=
2
1
2
θ
θ
θθ
µ
dsen
nI
B o
)cos(cos
2
12 θθ
µ
−=
nI
B o
( ) 2/322
2
2 ax
Ia
B o
+
=
µ

17. En el punto medio del solenoide, suponiendo que el solenoide es largo
comparado con a:
nIB oµ=
En el punto extremo del solenoide, suponiendo que el solenoide es largo
comparado con a:
nIB oµ2
1
=