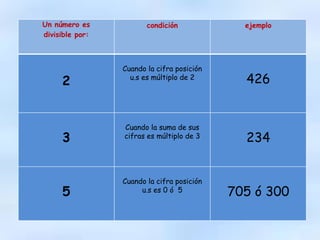
Este documento describe los conceptos de múltiplos, divisores, números primos y compuestos. Explica que los múltiplos de un número se obtienen al multiplicarlo por números naturales y que los divisores son aquellos números que dividen al número de forma exacta. También introduce métodos para determinar si un número es divisible por otro y cómo factorizar números expresándolos como producto de sus factores primos.

1. BLOQUE 4
“MULTIPLOS Y DIVISORES”
Por Ana Carolina Salvatore

2. MÚLTIPLOS
Los múltiplos de un número natural
cualquiera son todos aquellos que se
obtienen al multiplicar el número por:
0,1,2,3,4,5,...
Ejemplo: 4 x 3 = 12 decimos que 12
es múltiplo de 3 porque existe el 4 tal
que 4 x 3 = 12

3. Para indicar abreviadamente que un número es
múltiplo de otro, en símbolo anotamos así:
<4>= {0, 4, 8, 12, 16, 20, 24, 32, 40...}
<4> se lee conjunto de múltiplos de 4
Un número tiene infinitos múltiplos. Entonces…
los múltiplos se obtienen multiplicando
sucesivamente el número por los números
naturales (0, 1, 2, 3…)

4. DIVISORES
Pablo va a pegar 8 fotos en su álbum.
Quiere poner en cada hoja el mismo
número de fotos y que no le sobre ninguna
foto. ¿Cuántas fotos puede poner en cada
hoja?
Observa cómo puede repartir Eduardo las
fotos en partes iguales en las hojas del
álbum.

5. Pablo puede poner en cada hoja 1,2,4, u 8 fotos.
●Los números 1, 2, 4 y 8 son divisores de 8, porque al
dividir 8 entre cada uno de ellos la división es exacta.
● Los números 3, 5 , 6 y 7 no son divisores de 8, porque al
dividir 8 entre cada uno de ellos la división es entera.

6. Los divisores de un número natural “x” son todos aquellos
números menores o iguales que “x” que lo dividen
exactamente.
Ejemplo:
2 x 4 = 8
● decimos que 2 es divisor de 8, porque existe el 4 tal que
2 x 4 = 8
● decimos que 4 es divisor de 8, porque existe el 2 tal que
2 x 4 = 8

7. Anotamos así en símbolos:
∆15 = {1, 3, 5, 15 }
∆15 se lee conjunto de los divisores de 15
Ejemplos
∆2 = {1,2} ∆6 = {1,2,3,6} ∆9 = {1,3,9}

8. NÚMEROS PRIMOS Y
COMPUESTOS
Llamamos número primo al que solo tiene dos divisores: él mismo
y la unidad.
En cambio, un número es compuesto si tiene más de dos
divisores.
∆14= 1, 2, 7, 14
como tiene más de dos divisores, 14 es número compuesto;
∆7 = 1 , 7
como solo tiene dos divisores (él mismo y la unidad), 7 es número
primo.
El número 1 no se considera número primo ni compuesto, ya
que solo tiene un divisor: él mismo.

9. Tabla de criba de Erastóstenes

10. CRITERIOS DE DIVISIBILIDAD
Nos permiten descubrir si un número es divisible por otro sin
necesidad de hacer la división.

11. Un número es
divisible por:
condición ejemplo
2
Cuando la cifra posición
u.s es múltiplo de 2 426
3
Cuando la suma de sus
cifras es múltiplo de 3 234
5
Cuando la cifra posición
u.s es 0 ó 5 705 ó 300

12. FACTORIZACIÓN
Factorizar un
número es
expresarlo como
producto de sus
factores primos

13. Factorización de potencias de 10
La Factorización del 10 es 2 x 5, 2 es un número
primo y 5 es un número primo.
Para factorizar el 100 deducimos que es igual a
10 x 10, como conocemos la Factorización del 10
(2x5) concluimos a partir de esto que:
100 = 22 x 52
El mismo procedimiento usamos para 1.000,
10.000, etc
1.000= 23 x 53
10.000= 24 x 54

14. Factorizar mentalmente
250 = 2 x 5 x 5 x 5
primero factorizamos el cero por lo que anotamos 2x5
y luego factorizamos el 25 por lo que anotamos 5x5.
Concluimos que la Factorización del 250 es:
250= 2 x 53
Otros ejemplos:
2.800= 24 x 52 x 7
12.000= 25 x 53 x 3

15. Para factorizar con el algoritmo un número se
efectúan sucesivas divisiones entre sus
factores primos hasta obtener un uno como
cociente.
Para realizar las divisiones utilizaremos una
barra vertical, a la derecha escribimos los
factores primos y a la izquierda los
cocientes.
La factorización de 432 es:

16. Si queremos factorizar el 98, procedemos de la siguiente manera:
98 2
49 7
7 7
1
Pensamos un divisor de 98 que sea número primo, el 2
por ejemplo. Entonces pensamos 98:2=49.
Pensamos un divisor de 49 que sea número primo, el 7
por ejemplo. Entonces pensamos 49:7=7.
Como el número 7 es primo hacemos 7:7=1