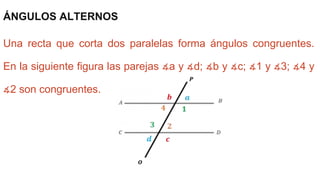
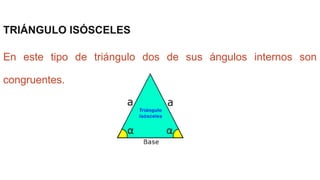
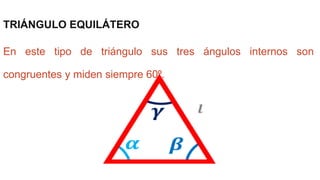
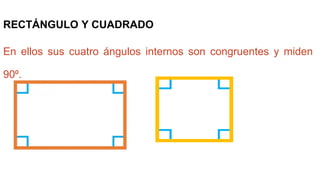
Este documento define ángulos congruentes como ángulos que miden lo mismo. Explica que los ángulos congruentes se aplican a la similitud y congruencia de figuras geométricas. Luego proporciona ejemplos de ángulos congruentes como ángulos verticales, ángulos alternos, y los ángulos internos de triángulos isósceles, equiláteros, rectángulos y cuadrados. Finalmente, describe cómo se puede determinar la congruencia de triángulos usando la congruencia de sus ángulos y lados.

1. ÁNGULOS CONGRUENTES
Alba Leclert

2. Se dice que α y β son ángulos congruentes si
miden lo mismo. Éstos tienen una amplia aplicación
en la similitud y congruencia de diferentes figuras
geométricas; podemos clasificar varias de estas
últimas en función de sus ángulos congruentes,
como es el caso de algunos triángulos.

3. DEFINICIÓN
Sea α y β dos ángulos, éstos serán ángulos
congruentes si tienen exactamente la misma
medida, es decir, α = β.

4. EJEMPLOS DE ÁNGULOS CONGRUENTES
ÁNGULOS VERTICALES
Cuando dos líneas de interceptan se forman 4 ángulos. Aquellos
que son opuestos uno al otro son ángulos verticales, éstos son
siempre congruentes. Por lo tanto, en la siguiente figura α = β y θ
= φ.

5. ÁNGULOS ALTERNOS
Una recta que corta dos paralelas forma ángulos congruentes.
En la siguiente figura las parejas ∡a y ∡d; ∡b y ∡c; ∡1 y ∡3; ∡4 y
∡2 son congruentes.

6. TRIÁNGULO ISÓSCELES
En este tipo de triángulo dos de sus ángulos internos son
congruentes.

7. TRIÁNGULO EQUILÁTERO
En este tipo de triángulo sus tres ángulos internos son
congruentes y miden siempre 60⁰.

8. RECTÁNGULO Y CUADRADO
En ellos sus cuatro ángulos internos son congruentes y miden
90⁰.

9. APLICACIÓN DE ÁNGULOS CONGRUENTES
Podemos determinar la congruencia de triángulos haciendo uso de sus ángulos junto a
la congruencia de sus lados. Dos triángulos serán iguales si se cumplen algunas de las
siguientes condiciones:
1. Si los tres lados de dos triángulos A y B son iguales, entonces éstos son
congruentes.
2. Si en dos triángulos A y B dos de sus lados y el ángulo formado por éstos son
iguales, entonces A y B son congruentes.
3. Si en dos triángulos A y B dos de sus ángulos son ángulos congruentes y el lado
comprendido entre éstos son iguales, entonces A y B son congruentes.