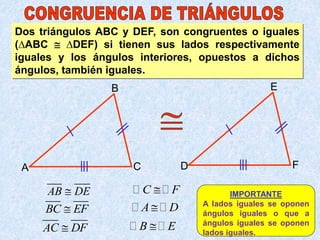
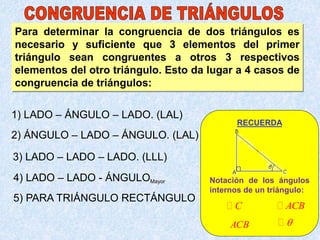
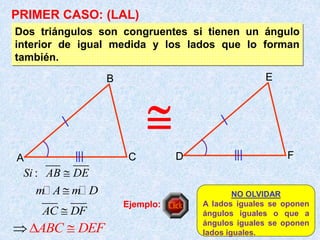
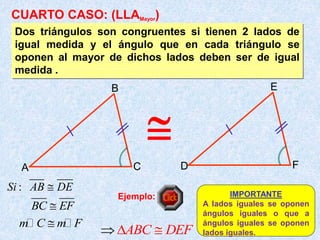
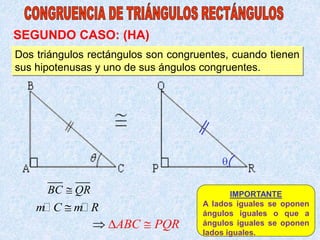
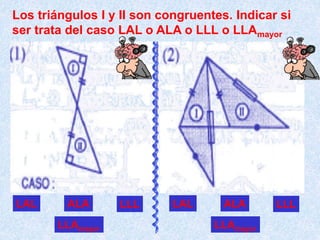
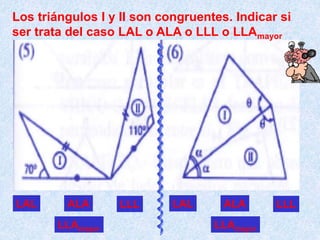
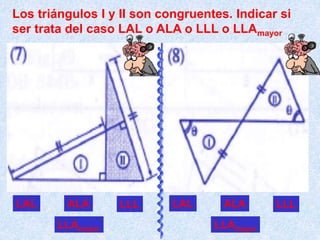
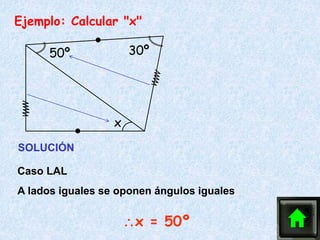
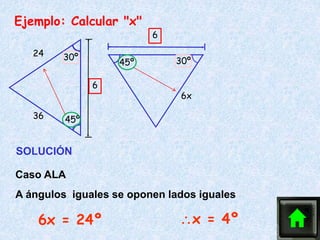
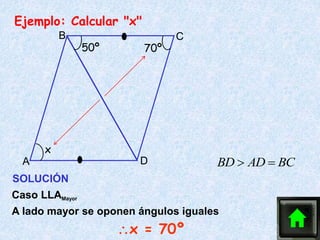
Este documento describe los cuatro casos de congruencia de triángulos: 1) Lado-Ángulo-Lado (LAL), 2) Ángulo-Lado-Ángulo (ALA), 3) Lado-Lado-Lado (LLL), y 4) Lado-Lado-Ángulo Mayor (LLAMayor). Para que dos triángulos sean congruentes, tres elementos correspondientes (lados u ángulos) deben ser iguales según uno de estos cuatro casos. El documento también explica la congruencia para triángulos rectángulos.