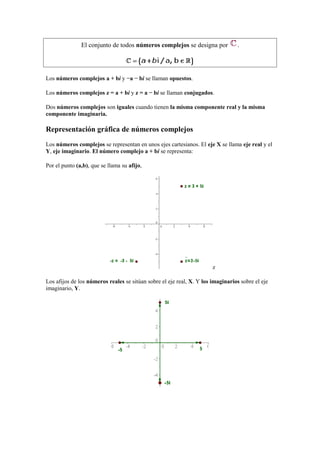
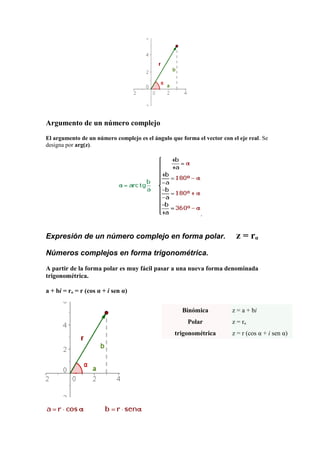
El documento describe los números complejos, incluyendo la unidad imaginaria i, números imaginarios en la forma binómica a + bi, operaciones como suma, resta, multiplicación y división, y representaciones como forma polar, trigonométrica y gráfica. Explica cómo convertir entre estas formas y conceptos como conjugados, opuestos e inversos. Finalmente, presenta ejemplos de cálculos con números complejos.

1. Números Complejos
Unidad imaginaria:Se llama así al número y se designa por la letra i.
Números imaginarios:Un número imaginario se denota por bi, donde :b es un número
real,e i es la unidad imaginaria.Con los números imaginarios podemos calcular raíces
con índice par y radicando negativo.
x2
+ 9 = 0
Potencias de la unidad imaginaria
i0
= 1 i1
= i i2
= −1 i3
= −i i4
= 1
Los valores se repiten de cuatro en cuatro, por eso, para saber cuánto vale una
determinada potencia de i, se divide el exponente entre 4, y el resto es el exponente de
la potencia equivalente a la dada.
i22
i22
= (i4
)5
· i2
= − 1
Números complejos en forma binómica
Al número a + bi le llamamos número complejo en forma binómica.
El número a se llama parte real del número complejo.
El número b se llama parte imaginaria del número complejo.
Si b = 0 el número complejo se reduce a un número real ya que a + 0i = a.
Si a = 0 el número complejo se reduce a bi, y se dice que es un número imaginario
puro.

2. El conjunto de todos números complejos se designa por .
Los números complejos a + bi y −a − bi se llaman opuestos.
Los números complejos z = a + bi y z = a − bi se llaman conjugados.
Dos números complejos son iguales cuando tienen la misma componente real y la misma
componente imaginaria.
Representación gráfica de números complejos
Los números complejos se representan en unos ejes cartesianos. El eje X se llama eje real y el
Y, eje imaginario. El número complejo a + bi se representa:
Por el punto (a,b), que se llama su afijo,
z
Los afijos de los números reales se sitúan sobre el eje real, X. Y los imaginarios sobre el eje
imaginario, Y.

3. Operaciones con números complejos en
la forma binómica
Suma y diferencia de números complejos
La suma y diferencia de números complejos se realiza sumando y restando partes reales
entre sí y partes imaginarias entre sí.
(a + bi) + (c + di) = (a + c) + (b + d)i (a + bi) − (c + di) = (a − c) + (b − d)i
(5 + 2i) + ( − 8 + 3i) − (4 − 2i) = (5 − 8 − 4) + (2 + 3 + 2)i = −7 + 7i
Multiplicación de números complejos
El producto de los números complejos se realiza aplicando la propiedad distributiva del
producto respecto de la suma y teniendo en cuenta que i2
= −1.
(a + bi) · (c + di) = (ac − bd) + (ad + bc)i
(5 + 2i) · (2 − 3i) =10 − 15i + 4i − 6 i2
= 10 − 11i + 6 = 16 − 11i
División de números complejos
El cociente de números complejos se hace racionalizando el denominador; esto es,
multiplicando numerador y denominador por el conjugado de éste.
Números complejos en forma polar
Módulo de un número complejo
El módulo de un número complejo es el módulo del vector determinado por el origen de
coordenadas y su afijo. Se designa por |z|.

4. Argumento de un número complejo
El argumento de un número complejo es el ángulo que forma el vector con el eje real. Se
designa por arg(z).
.
Expresión de un número complejo en forma polar. z = rα
Números complejos en forma trigonométrica.
A partir de la forma polar es muy fácil pasar a una nueva forma denominada
trigonométrica.
a + bi = rα = r (cos α + i sen α)
Binómica z = a + bi
Polar z = rα
trigonométrica z = r (cos α + i sen α)

5. Ejemplos: Pasar a la forma polar y trigonométrica:
z = 260º
= 2(cos 60º + i sen 60º)
z = 2120º
=2(cos 120º + i sen 120º)
z = 2240º
=2(cos 240º + i sen 240º)
z = 2300º
=2(cos 300º + i sen 300º)
z = 2
z = 20º
=2(cos 0º + i sen 0º)
z = −2
z = 2180º
=2(cos 180º + i sen 180º)
z = 2i
z = 290º
=2(cos 90º + i sen 90º)
z = −2i
z = 2270º
=2(cos 270º + i sen 270º)

6. Pasar a la forma binómica:
z = 2120º
Para pasar de la forma polar a la binómica, tenemos que pasar en primer lugar a la forma
trigonométrica
rα = r (cos α + i sen α)
z = 2 · (cos 120º + i sen 120º)
Números complejos iguales
Dos números complejos son iguales si tienen el mismo módulo y el mismo argumento.
Números complejos conjugados
Dos números complejos son conjugados si tienen el mismo módulo y el opuestos sus
argumento.
Números complejos opuestos
Dos números complejos son opuestos si tienen el mismo módulo y sus argumentos se
diferencian en π radianes.

7. Números complejos inversos
El inverso de un número complejo no nulo, tiene por módulo el inverso del módulo y por
argumento su opuesto.
Producto y cociente de complejos en forma polar
La multiplicación de dos números complejos es otro número complejo tal que:
Su módulo es el producto de los módulos. Su argumento es la suma de los argumentos.
645° · 315° = 1860°
La división de dos números complejos es otro número complejo tal que:
Su módulo es el cociente de los módulos. Su argumento es la diferencia de los argumentos.
645° : 315° = 230°
Interpretación geométrica del producto de números complejos.
Al multiplicar un número complejo z = rα por 1β se gira z un ángulo β alrededor del origen.
rα · 1β = rα + β
Potencia de número complejo

8. La potencia enésima de número complejo es otro número complejo tal que:
Su módulo es la potencia n-ésima del módulo.Su argumento es n veces el argumento dado.
(230°)4
= 16120°
Esta operación conviene hacerla siempre en forma polar.
A partir del modo de cálculo de las potencias de números complejos se obtiene la Fórmula
de Moivre
Raíz de números complejos
La raíz enésima de número complejo es otro número complejo tal que:
Su módulo es la en raíz enésima del módulo.
Su argumento es:
k = 0,1 ,2 ,3, … (n-1)
Al igual que las potencias, las raíces conviene que se hagan expresando el número
complejo en forma polar.

9. EJERCICIOS
1 Calcular todas las raíces de la ecuación: x6
+ 1 = 0
2 Realiza las siguientes operaciones:
3 Resuelve la siguiente raíz, expresando los resultados en forma polar.
4Escribe una ecuación de segundo grado que tenga por soluciones 1 + 2i y su conjugado.
5Calcula , dando el resultado en forma polar.

10. 6 Calcula el valor de , y representa los afijos de sus raíces cúbicas.
7 Expresa en forma polar y binómica un complejo cuyo cubo sea:
8 Escribe en las formas polar y trigonométrica, los conjugados y los opuestos de:
14 + 4i
2−2 + 2i
9 Calcular todas las raíces de la ecuación: x5
+ 32 = 0
10Calcula k para que el número complejo que obtenemos al dividir esté representado en
la bisectriz del primer cuadrante.
11 Halla el valor de k para que el cociente sea:
1.-Un número imaginario puro. 2.-Uno número real.
12 Se considera el complejo 2 + 2 i, se gira 45° alrededor del origen de coordenadas en
sentido contrario a las agujas del reloj. Hallar el complejo obtenido después del giro.
13 Halla las coordenadas de los vértices de un hexágono regular de centro el origen de
coordenadas, sabiendo que uno de los vértices es el afijo del complejo 190°.
14 Determina el valor de a y b para que el cociente sea igual a:
15 Cuáles son las coordenadas del punto que se obtiene al girar 90°, en sentido antihorario
alrededor del origen, el afijo del complejo 2 + i.
16 Halla las coordenadas de los vértices de un cuadrado de centro el origen de coordenadas,
sabiendo que uno de los vértices es el punto (0, −2).
17 La suma de los componentes reales de dos números complejos conjugados es seis, y
la suma de sus módulos es 10. Determina esos complejos en la forma binómica y polar.