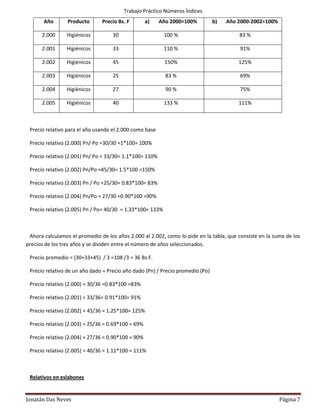
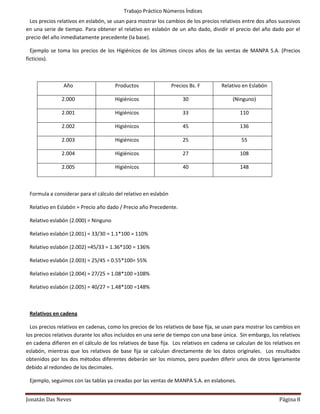
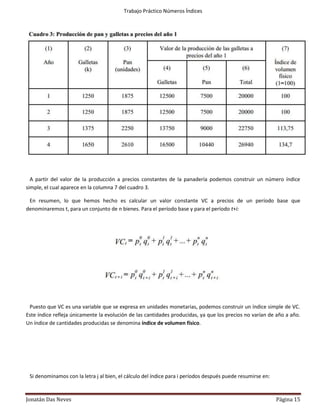
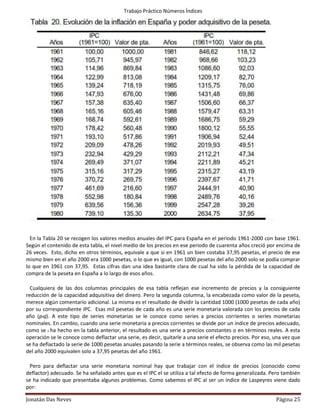
Este documento explica los números índices y sus diferentes tipos. Los números índices son medidas estadísticas que permiten caracterizar la evolución de una magnitud en dos períodos de tiempo. Existen índices simples para un solo artículo y índices compuestos para grupos de artículos. Los índices simples se calculan dividiendo cada valor por el valor base y multiplicando por 100. Los documentos también explica índices de base fija, en eslabones y en cadenas para series con múltiples años.