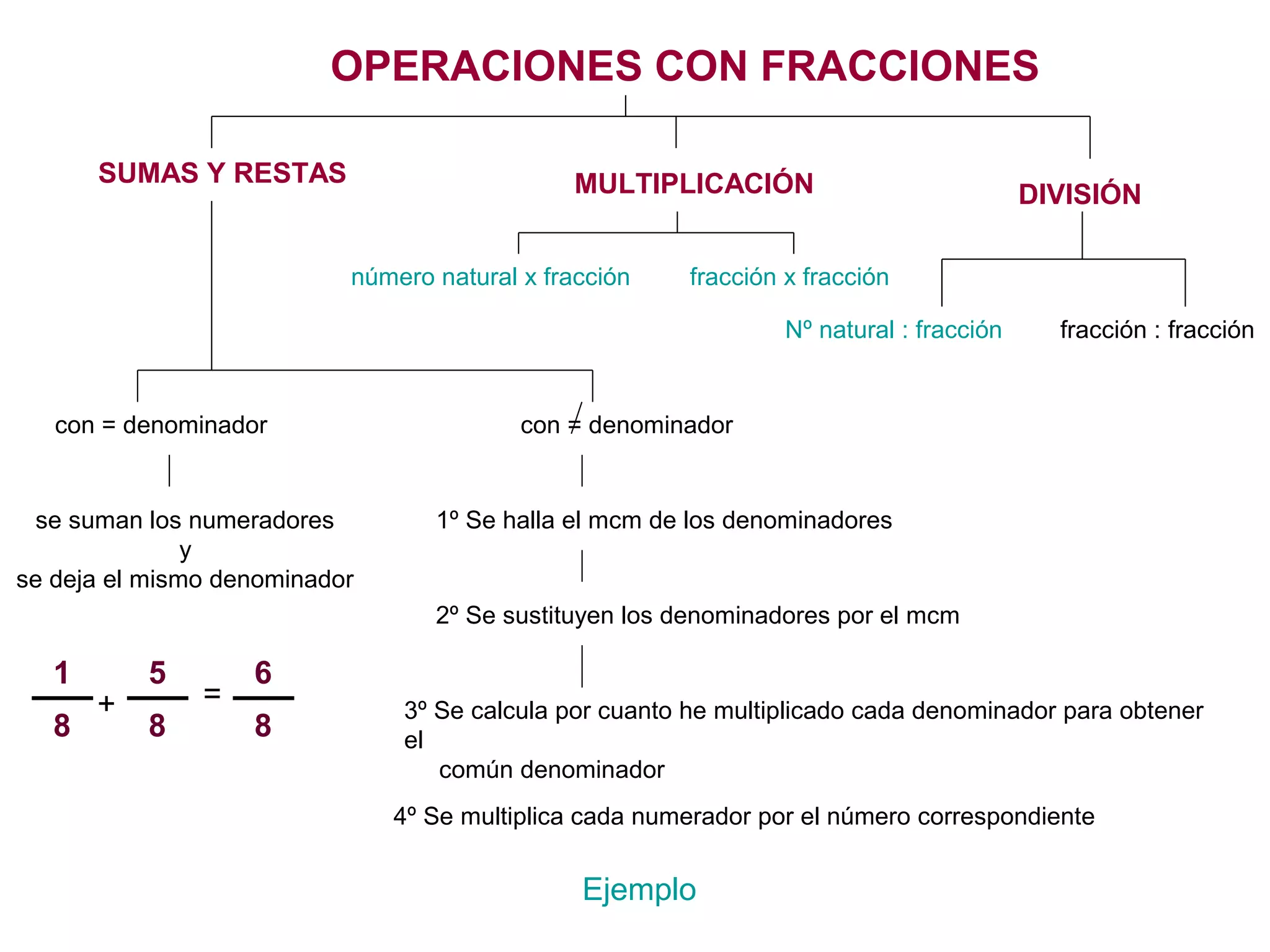
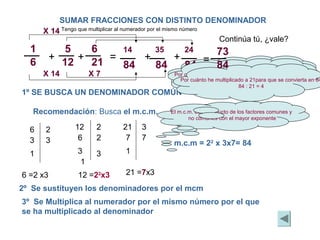
El documento proporciona instrucciones para realizar operaciones con fracciones, incluyendo sumas, restas, multiplicación y división. Explica que para sumar o restar fracciones con distintos denominadores, primero se debe encontrar un denominador común y luego sumar o restar los numeradores. Para multiplicar fracciones, el numerador se multiplica por el otro numerador y el denominador se multiplica por el otro denominador. Para dividir fracciones, la fracción dividendo se multiplica por el inverso de la fracción divisor.

1. OPERACIONES CON FRACCIONES
SUMAS Y RESTAS
con = denominador con = denominador
se suman los numeradores
y
se deja el mismo denominador
1º Se halla el mcm de los denominadores
1
8
+
5
8
=
6
8
2º Se sustituyen los denominadores por el mcm
3º Se calcula por cuanto he multiplicado cada denominador para obtener
el
común denominador
4º Se multiplica cada numerador por el número correspondiente
MULTIPLICACIÓN DIVISIÓN
Ejemplo
número natural x fracción fracción x fracción
Nº natural : fracción fracción : fracción

2. 1
6
+
5
12
+
6
21
SUMAR FRACCIONES CON DISTINTO DENOMINADOR
1º SE BUSCA UN DENOMINADOR COMÚN
Recomendación: Busca el m.c.m.
3
7 7
21
1
6 =2 x3 21 =7x3
El m.c.m. es el producto de los factores comunes y
no comunes con el mayor exponente
m.c.m = 22
x 3x7= 84
12 =22
x3
=
2º Se sustituyen los denominadores por el mcm
84
+
84
+
84
3º Se Multiplica al numerador por el mismo número por el que
se ha multiplicado al denominador
X 14
Continúa tú, ¿vale?
2
3 3
6
1
2
2
12
6
3 3
1
Por cuánto he multiplicado a 6 para que se convierta en 84
84 : 6 = 14
X 14 Tengo que multiplicar al numerador por el mismo número
Por cuánto he multiplicado a 12 para que se convierta en 84
84 : 12 = 7
X 7
14 35
Por cuánto he multiplicado a 21para que se convierta en 84
84 : 21 = 4
24
=
73
84

3. MULTIPLICACIÓN
1 – fracción x número natural
Se multiplica el número por el numerador y se pone el mismo denominador
2 – Fracción x fracción
5
7
X
2
3
=
5x2
7x3
El resultado es una fracción cuyo numerador es el producto de los numeradores y cuyo
denominador es el producto de los denominadores
=
10
21
1
6
X 7 =
7
6
3
6
7 X; =
21
6

4. DIVISIÓN
Se multiplica el dividendo por el inverso del divisor
2 – Fracción : fracción
5
7
:
2
3
=
5
7
=
15
14
2 – número natural : fracción
1 – fracción : número natural
1
6
: 7 =
1
6
X
;
X
1
7
=
1
42
5
6
7 : =
6
5
7 X =
42
5
Se multiplica el dividendo por el inverso del divisor
Se multiplica el dividendo por el inverso del divisor
3
2