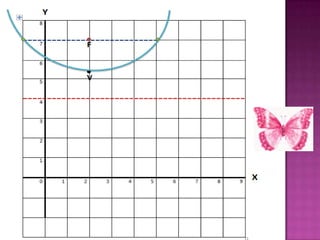
Este documento resume las propiedades básicas de las parábolas. Define una parábola como el lugar geométrico de puntos que equidistan de una recta directriz y un punto foco. Detalla las características clave de una parábola incluyendo la directriz, foco, eje, vértice, cuerdas, lado recto y radio vector. Además, presenta las ecuaciones generales de una parábola y resuelve dos ejemplos para hallar ecuaciones de parábolas específicas.

1. MATEMÁTICA APLICADA
VERÓNICA AGUIRRE
JUDITH MAIGUA
4to. Ingeniería Comercial A

2.  Dados en un plano una recta y un punto exterior, se llama
parábola al lugar geométrico de los puntos del plano que
equidistan de la recta llamada Directriz, y del punto o
Foco. La Directriz se designa con la letra D; el Foco de la
parábola se designa con la letra F.
 Es el lugar geométrico de un punto que se mueve de tal
manera que la distancia del punto a una recta fija es igual a
la distancia a un punto fijo.

3. Y D L B
DIRECTRIZ (D).- la recta fija de
la parábola. C
FOCO (F).- es el punto fijo de la
parábola. V F
E
EJE (E).- es la recta que pasa
por el foco y es perpendicular a B’
la directriz. -X N X
R C’
VÉRTICE (V).- es el punto donde
la parábola le corta al eje. El
vértice está en el punto medio -Y
entre la distancia de la directriz
y el foco. Es el punto más
extremo de la parábola.

4. CUERDA (BB’).- Es un segmento D L B
Y
que une dos puntos cualquiera C
en una parábola. Este segmento
no pasa por el foco.
V F
CUERDA FOCAL (CC’).- Es el E
segmento que va a unir dos
puntos que pasa por el foco de B’
la parábola.
-X N X
LADO RECTO (LR).- es una R C’
cuerda focal perpendicular al
eje de la parábola y paralela a
la directriz. -Y
RADIO VECTOR (FN).- es el segmento que
une el foco con un punto de la parábola.
Cada radio tendrá diferente dimensión solo
habrá un par de igual dimensión.

5. 

6. 

7.  ECUACIÓN DE LA PARÁBOLA CON VÉRTICE EN
(H,K) QUE SE ABRE A LA DERECHA O IZQUIERDA.
(y-k)2 = ± 4a (x-h)
 ECUACIÓN DE LA PARÁBOLA CON VÉRTICE EN
(H,K) QUE SE ABRE HACIA ARRIBA O HACIA
ABAJO.
(x-h)2 = ± 4a(y-k)

8.  Hallar la ecuación de la parábola de vértice
el punto (3,2) y foco el punto (5,2).
DATOS:
a=2 (y-k)2 = 4a(x-h)
v=(3,2) (y-2)2 = 4*2(x-3)
f=(5,2) y2-4y+4 = 8x-24
y2-4y-8x+28 = 0

10.  Hallar la ecuación de la parábola cuyo lado
recto es el segmento comprendido entre los
puntos (-1,7) y (5,7)
DATOS:
a= 1,5
(x-h)2 = 4a (y-k)
V(2; 5,5) (x-2)2 = 4(1,5) (y-5,5)
F(2,7) (x2-4x+4) = 6y+33
x2-4x-6y+37 = 0