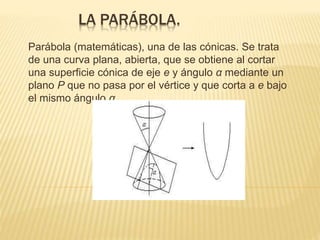
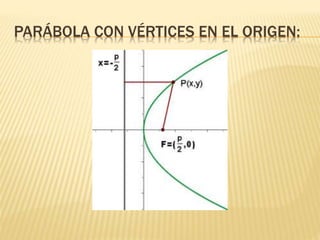
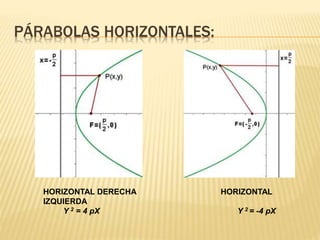
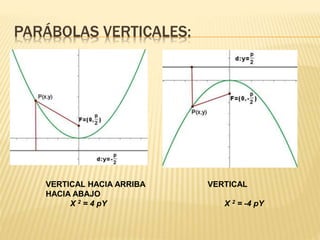
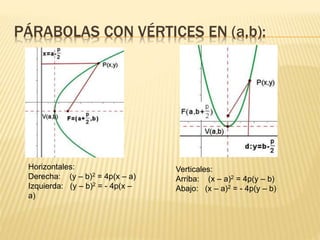
La parábola es una curva plana definida como el lugar geométrico de los puntos equidistantes de un punto fijo llamado foco y de una recta fija llamada directriz. Presenta elementos como el foco, directriz, eje y vértice. Tiene propiedades como que los rayos paralelos al eje se reflejan pasando por el foco, lo que se usa en faros de autos y antenas parabólicas. Se representa mediante ecuaciones que relacionan las coordenadas de sus puntos.

1. LA PARÁBOLA.
Parábola (matemáticas), una de las cónicas. Se trata
de una curva plana, abierta, que se obtiene al cortar
una superficie cónica de eje e y ángulo α mediante un
plano P que no pasa por el vértice y que corta a e bajo
el mismo ángulo α.

2. LA PARÁBOLA
 La parábola se puede definir como el lugar geométrico de
los puntos del plano que equidistan de un punto fijo llamado
foco, y de una recta fija llamada directriz.
 La distancia entre el foco y la directriz se llama parámetro
(p)
 Además del foco, F, y de la directriz, d, en una parábola
destacan los siguientes elementos:
•Eje de la parábola, e.
•Vértice, V.
• Distancia de F a d, p.

3. LA PARÁBOLA
 Si un rayo es paralelo al eje de la parábola, se refleja en
ésta pasando por su foco. Y, viceversa, si pasa por su
foco, se refleja en la parábola y se aleja paralelo al eje.
 Esta propiedad se utiliza, por ejemplo, para fabricar los
faros de forma parabólica de los automóviles (el punto
luminoso está en el foco y, por tanto, el haz de rayos es
paralelo al eje) y las antenas para captar emisiones
(dirigidas hacia el lugar de donde proviene la emisión,
concentra en el foco todos los rayos que recibe).
Parábolas son también las trayectorias de cualquier
cuerpo (bola, pelota, chorro de agua…) que cae atraído
por la tierra.

4. LA PARÁBOLA
EJE
DIRECTRIZ
l
P’
P
o
.
v o
F
Fig. 1
Si P es un punto en el plano y P’ es
el punto sobre l determinado por la
recta perpendicular a l y que pasa
por P (Fig. 1), entonces, según la
definición de parábola, P está en la
parábola si y solo si
d ( P , F) = d ( P, P’ ).
El punto P puede estar en cualquier
parte sobre la curva en la fig. 1
La recta que pasa por F y es
perpendicular a la directriz se llama
eje de la parábola.
El punto V sobre el eje y que esta
a la misma distancia de F y de l, se
llama Vértice de la parábola.

5. COMPONENTES DE LA PARÁBOLA:
 Foco: Es el punto fijo F.
 Directriz : Es la recta fija D.
 Parámetro : Es la distancia del foco a la directriz, se designa por
la letra p.
 Eje : Es la recta perpendicular a la directriz que pasa por el foco.
 Vértice: Es el punto de intersección de la parábola con su eje.
 Radio vector : Es un segmento que une un punto cualquiera de
la parábola con el foco.

6. PARÁBOLA CON VÉRTICES EN EL ORIGEN:

7. PÁRABOLAS HORIZONTALES:
HORIZONTAL DERECHA HORIZONTAL
IZQUIERDA
Y 2 = 4 pX Y 2 = -4 pX

8. PARÁBOLAS VERTICALES:
VERTICAL HACIA ARRIBA VERTICAL
HACIA ABAJO
X 2 = 4 pY X 2 = -4 pY

9. PÁRABOLAS CON VÉRTICES EN (a,b):
Horizontales:
Derecha: (y – b)2 = 4p(x – a)
Izquierda: (y – b)2 = - 4p(x –
a)
Verticales:
Arriba: (x – a)2 = 4p(y – b)
Abajo: (x – a)2 = - 4p(y – b)

10. ECUACION ESTANDAR Y GENERAL:
POSICIÓN ECUACIÓN
ESTÁNDAR
ECUACIÓN
GENERAL
HORIZONTAL (y – b)2 = +/- 4p(x –
a)
y2 + Dx + Ey + F = 0
VERTICAL (x – a)2 = +/- 4p(y –
b)
x2 + Dx + Ey + F = 0

11. GRAFICA EJEMPLO 1 LA PARÁBOLA
y
F(- 3/2, 0 )
X = 3/2
y2 = - 6x
.
 1. Encontrar el foco y la
directriz de la parábola con la
ecuación y2 = - 6x y trazar su
gráfica.
SOLUCION.
La ecuación y2 = - 6x , tiene la
forma (ii) de los teoremas
anteriores con 4p = - 6, y por
lo tanto p = - 3/2.
Resulta que el foco es F (p,0),
es decir , F( - 3/2 , 0).
La ecuación de la directriz es
x = - p , o bien
x = - ( -3/2), x= 3/2.

12. EJEMPLO 2:
 Encontrar la ecuación de la parábola con eje paralelo al eje “y” y que pasa por
los puntos P(-2, 1); Q(4, -5) y R(10, 1).
Solución:
Los tres puntos pertenecen a la parábola, por lo que deben cumplir con la
ecuación:
x2 + Dx + Ey + F = 0. (por ser parábola horizontal)
Tendremos entonces tres ecuaciones con tres incógnitas, D, E y F.
Escribamos las ecuaciones sustituyendo los valores de las coordenadas de los
puntos.
1) (-2)2 + (-2)D + (1)E + F = 0 -2D + E + F = -4
2) (4)2 + (4) D + (-5)E + F = 0 4D – 5E + F = -16
3) (10)2 + (10)D + E + F = 0 10D + 10E + F = -100
Al resolver el sistema, obtenemos los resultados: D= - 8, E= - 6, F = - 14.
La ecuación de la parábola es: x2 – 8x – 6y – 14 = 0.
Al expresar la ecuación en su forma estándar es : (x – 4)2 = 6( y + 5)

13. EJEMPLO 3:
Una sección de un puente colgante tiene un peso uniformemente
distribuido entre dos torres gemelas que distan 400 pies una de
otra; y se elevan 90 pies sobre una carretera horizontal. Un cable
suspendido entre los extremos superiores de las torres tiene
forma parabólica y su punto medio se encuentra a 10 pies por
arriba de la carretera, considere los ejes coordenados que se
muestran:
 a) encuentre la ecuación de la parábola respectiva
Ecuación estándar: (x- a)2 = 4p(y – b)
vértice (0, 10) p = 10
Ecuación: x2= 40 (y – 10)
 b) establezca una integral que de la longitud del cable.
Esta queda de la forma:

14. EJEMPLO 3: