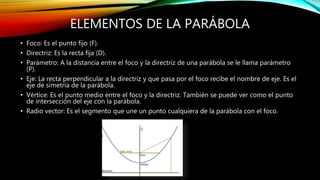
Este documento define la parábola como el lugar geométrico de todos los puntos equidistantes de un punto fijo llamado foco y una recta fija llamada directriz. Explica los elementos de la parábola como el foco, directriz, parámetro, eje, vértice y radio vector. Luego proporciona las ecuaciones canónicas de la parábola para diferentes posiciones del vértice y eje de simetría, y concluye dando la ecuación general de la parábola.

1. LA PARÁBOLA
República Bolivariana de Venezuela
Ministerio Del Poder Popular Para La Educación
U.E. Colegio “Del Santísimo”
Barquisimeto, Edo-Lara.
Integrantes:
-Elorza L. #16
-Guedez O. #21
-Perez M. #34
Profesor:
-Prof. Miguel Gerdez
Año y sección:
-5to “B”

2. DEFINICIÓN COMO LUGAR GEOMÉTRICO
• La parábola es el lugar geométrico de todos los puntos del plano que equidistan de
un punto fijo llamado foco y de una recta fija llamada directriz.

3. ELEMENTOS DE LA PARÁBOLA
• Foco: Es el punto fijo (F).
• Directriz: Es la recta fija (D).
• Parámetro: A la distancia entre el foco y la directriz de una parábola se le llama parámetro
(P).
• Eje: La recta perpendicular a la directriz y que pasa por el foco recibe el nombre de eje. Es el
eje de simetría de la parábola.
• Vértice: Es el punto medio entre el foco y la directriz. También se puede ver como el punto
de intersección del eje con la parábola.
• Radio vector: Es el segmento que une un punto cualquiera de la parábola con el foco.

4. ECUACION CANÓNICA DE LA PARÁBOLA CON
VERTICE EN (0,0) Y EJE DE SIMETRIA AL EJE “X”
La ecuación de una parábola de vértice en el origen y eje el eje 𝑋, es 𝑦2= 4𝑝𝑥en donde
el foco es el punto (𝑝 , 0) y la ecuación de la directriz es 𝑥 = − 𝑝. Si 𝑝 > 0, la parábola
se abre hacia la derecha; si 𝑝 < 0, la parábola se abre hacia la izquierda.

5. ECUACION CANÓNICA DE LA PARÁBOLA CON
VERTICE EN (0,0) Y EJE DE SIMETRIA AL EJE “Y”
Si el eje de una parábola coincide con el eje 𝑌 , y el vértice está en el origen, su
ecuación es 𝑥 2 = 4𝑝𝑦 en donde el foco es el punto (0, 𝑝), y la ecuación de la directriz
es 𝑦 = −𝑝. Si 𝑝 > 0, la parábola se abre hacia arriba; si 𝑝 < 0, la parábola se abre hacia
abajo.

6. ECUACION CANÓNICA DE LA PARÁBOLA CON
VERTICE EN (H,K) Y EJE DE SIMETRIA PARALELO AL EJE
“X”
La ecuación de una parábola con vértice (ℎ, 𝑘) y eje paralelo al eje 𝑋, es de la forma (𝑦
− 𝑘)2 = 4𝑝 (𝑥 − ℎ) Siendo |𝑝| la longitud del segmento del eje comprendido entre el
foco y el vértice. Si 𝑃 > 0, la parábola se abre hacia la derecha; si 𝑃 < 0, la parábola se
abre hacia la izquierda.

7. ECUACION CANÓNICA DE LA PARÁBOLA CON
VERTICE EN (H,K) Y EJE DE SIMETRIA PARALELO AL EJE
“Y”
Si el vértice es el punto (ℎ, 𝑘) y el eje de la parábola es paralelo al eje 𝑌, su ecuación es
de la forma (𝑥 − ℎ) 2 = 4𝑝 (𝑦 − ℎ). Si 𝑃 > 0, la parábola se abre hacia arriba; si 𝑃 < 0, la
parábola se abre hacia abajo.
http://www.galileo2.com.mx/Tolima/images/S3_Parabolas_e_Hiperbolas.pdf

8. ECUACIÓN GENERAL DE LA PARÁBOLA
Aceptamos el significado de general como la parábola cuyo vértice no está situado en
el origen de coordenadas.
Supongamos que el vértice de una parábola cuando su eje focal es paralelo al eje Y se
halla situado en el punto (h,k).
En este caso tendremos que trasladar el vértice al nuevo punto quedándonos
establecida la fórmula:
Hacemos operaciones:
Damos valores a:
Sustituyendo estos valores en (I) obtenemos la ecuación general de la parábola:
Cuando su eje focal es paralelo al eje X se halla situado en el punto (h, k) la fórmula es:

9. EJERCICIOS
Una parábola tiene su foco en el punto F(5,0) y su vértice en V(1,0). ¿Cuál es su
ecuación? Dibuja la parábola.
http://www.aulafacil.com/cursos/l10814/ciencia/matemati
cas/matematicas-conicas/ecuacion-de-la-parabola-en-la-
forma-general