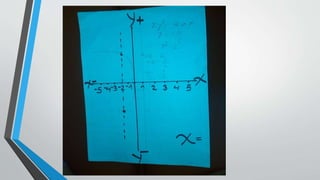
El documento define una parábola como un lugar geométrico de puntos en un plano que están a igual distancia de un punto fijo llamado foco y de una recta fija llamada directriz. Explica que una parábola tiene un vértice, un eje de simetría que pasa por el vértice y el foco, y una ecuación canónica de la forma y2 = 4px cuando el vértice está en el origen y el eje de simetría es el eje x. También muestra cómo derivar la ecuación de una parábola

1. La Parábola
Integrantes:
Jessica Barrera
Yuselfi Sierra
Ana Karina Hernández
Grado: 11-1

2. ¿Qué es la Parábola?
Es un lugar geométrico de los puntos (x,y) del plano que equivalen de
una recta fija llamada Directriz y de un punto fijo llamado Foco.

3. Elementos de la Parábola.
• La recta Fija L se llama directriz y tiene ecuación en x= -c
• El punto fijo F se llama foco y tiene coordenadas (a,0).
• P es un punto cualquiera y tiene coordenadas en (x,y).
• El eje donde se encuentra ubicado el foco se denominada eje de simetría
el cual es el eje X.

4. • El punto V en el que la parábola corta al eje de simetría se llama vértice y
tiene coordenadas (0,0).
• La distancia entre el vértice y la directriz es la misma distancia que hay
entre el vértice y el foco, dicha distancia es a.
• El segmento de recta AB que pasa por el foco y es perpendicular al eje de
simetría se denomina Latus rectum.

5. Ecuación Canónica de una parábola con
vértice en (0,0) y el eje de simetría al eje x..
(𝑥 − 𝑝)2 + 𝑦2 = 𝑥 + 𝑝
Ahora elevamos ambos miembros al cuadrado.
(𝑥 − 𝑝)2
+𝑦2
= (𝑥 + 𝑝)2
𝑥2
− 2xp + 𝑝2
+ 𝑦2
= 𝑥2
+ 2𝑥𝑝 + 𝑝2
𝑥2
− 2𝑥𝑝 − 𝑝2
− 𝑝2
+ 𝑦2
− 𝑥2
= 2𝑥𝑝 + 2𝑥𝑝
𝑦2
= 4𝑝𝑥
Vértice(0,0)
Foco(P,0)
Eje de Simetría (X)

6. Ecuación de la Parábola con vértice (0,0) y
eje de simetría eje Y.
• 𝑥 − 02 + (𝑦 − 𝑝)2 = 𝑦 + 𝑝
• Elevando al cuadrado
• 𝑥2 + 𝑦2 − 2𝑝𝑦 + 𝑝2 = 𝑦2 + 2𝑝𝑦 + 𝑝2
• 𝑥2
+ 𝑦2
+ 𝑝2
− 𝑦2
− 𝑝2
= 2𝑝𝑦 + 2𝑝𝑦
• 𝑥2 = 4𝑝𝑦
• El eje de simetría Y

7. 4 𝑦2 = 8𝑥
𝑦2 =
8𝑥
4
𝑦2
= 2𝑥
1
2
, 0
X=−
1
2
4 a=2
a=
2
4
a=
1
2

9. Tarea
• 6 𝑦2 = 8𝑥
• 16𝑥2 = 6𝑦