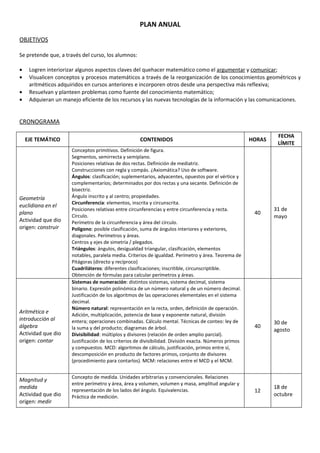
Este plan anual tiene como objetivos que los alumnos logren interiorizar aspectos claves del quehacer matemático como argumentar y comunicar, visualicen conceptos geométricos y aritméticos de manera reflexiva, resuelvan y planteen problemas, y adquieran un manejo eficiente de las tecnologías. El cronograma presenta los contenidos de geometría euclidiana, aritmética e introducción al álgebra, y magnitud y medida que se verán, junto con las fechas límite. La evaluación considerará actitudes científicas

1. PLAN ANUAL
OBJETIVOS
Se pretende que, a través del curso, los alumnos:
• Logren interiorizar algunos aspectos claves del quehacer matemático como el argumentar y comunicar;
• Visualicen conceptos y procesos matemáticos a través de la reorganización de los conocimientos geométricos y
aritméticos adquiridos en cursos anteriores e incorporen otros desde una perspectiva más reflexiva;
• Resuelvan y planteen problemas como fuente del conocimiento matemático;
• Adquieran un manejo eficiente de los recursos y las nuevas tecnologías de la información y las comunicaciones.
CRONOGRAMA
FECHA
EJE TEMÁTICO CONTENIDOS HORAS
LÍMITE
Conceptos primitivos. Definición de figura.
Segmentos, semirrecta y semiplano.
Posiciones relativas de dos rectas. Definición de mediatriz.
Construcciones con regla y compás. ¿Axiomática? Uso de software.
Ángulos: clasificación; suplementarios, adyacentes, opuestos por el vértice y
complementarios; determinados por dos rectas y una secante. Definición de
bisectriz.
Geometría Ángulo inscrito y al centro; propiedades.
Circunferencia: elementos, inscrita y circunscrita.
euclidiana en el
Posiciones relativas entre circunferencias y entre circunferencia y recta. 31 de
plano 40
Círculo. mayo
Actividad que dio Perímetro de la circunferencia y área del círculo.
origen: construir Polígono: posible clasificación, suma de ángulos interiores y exteriores,
diagonales. Perímetros y áreas.
Centros y ejes de simetría / plegados.
Triángulos: ángulos, desigualdad triangular, clasificación, elementos
notables, paralela media. Criterios de igualdad. Perímetro y área. Teorema de
Pitágoras (directo y recíproco)
Cuadriláteros: diferentes clasificaciones; inscritible, circunscriptible.
Obtención de fórmulas para calcular perímetros y áreas.
Sistemas de numeración: distintos sistemas, sistema decimal, sistema
binario. Expresión polinómica de un número natural y de un número decimal.
Justificación de los algoritmos de las operaciones elementales en el sistema
decimal.
Número natural: representación en la recta, orden, definición de operación.
Aritmética e Adición, multiplicación, potencia de base y exponente natural, división
introducción al entera; operaciones combinadas. Cálculo mental. Técnicas de conteo: ley de 30 de
álgebra la suma y del producto; diagramas de árbol. 40
agosto
Actividad que dio Divisibilidad: múltiplos y divisores (relación de orden amplio parcial).
origen: contar Justificación de los criterios de divisibilidad. División exacta. Números primos
y compuestos. MCD: algoritmos de cálculo, justificación, primos entre sí,
descomposición en producto de factores primos, conjunto de divisores
(procedimiento para contarlos). MCM: relaciones entre el MCD y el MCM.
Concepto de medida. Unidades arbitrarias y convencionales. Relaciones
Magnitud y
entre perímetro y área, área y volumen, volumen y masa, amplitud angular y
medida 18 de
representación de los lados del ángulo. Equivalencias. 12
Actividad que dio Práctica de medición. octubre
origen: medir

2. EVALUACIÓN
• Se ponderará la actitud científica, crítica y positiva hacia la disciplina (elementos imprescindibles para lograr un
desempeño aceptable en el curso) y una actitud de colaboración, tolerancia y respeto hacia los pares. Estos
aspectos serán observado a diario en las intervenciones orales y actividades grupales.
• Las fechas de las instancias formales se informan el primer día de clase:
FECHA ACTIVIDAD
22 marzo Diagnóstico
24/26 abril Presentaciones orales (guía con preguntas) – individual
28/29 mayo Escrito
21 junio Entrega de selección de problemas - individual
5/07 Parcial
30/31 julio – 2 agosto Presentaciones orales (preparación tema breve) – en equipos
27/28 agosto Escrito
Entrega de tarea en equipo (uso de software informático) – en
27 setiembre
equipos
4/10 Parcial
BIBLIOGRAFÍA:
• Alsina, C. y otros. (1997)¿Por qué geometría? Editorial Síntesis. Madrid.
• Belcredi, Luis y otros (1999) Geometría. Un curso de geometría métrica para el segundo ciclo. Ediciones
de La Plaza. Montevideo.
• Bolt, B. (1987-88) Divertimentos matemáticos. Actividades matemáticas. Más actividades matemáticas.
Editorial Labor. Barcelona.
• Borbonet, M. y otros. (2011) Matemática 1, 2 y 3. Grupo Botadá. Fin de Siglo. Montevideo.
• Castelnuovo, Emma (1968) Geometría intuitiva. Editorial Labor. Barcelona.
• Cólera, José; de Guzmán, Miguel (1994) Bachillerato, Matemática I. Editorial Anaya. Barcelona.
• Consejo Nacional de Educación. (1983) Lugares geométricos. Método de los lugares. Aplicaciones.
Montevideo.
• Coxeter, H. S. M. (1971) Fundamentos de Geometría. Edit. Limusa – Wiley, S.A. México.
• Fernández, Cecilia y otros Matemática 1ª, 2º y 3° C.B.U. Monteverde. Montevideo.
• Gil, Omar (2003) Números naturales, racionales y reales, y el sistema de numeración en
Publicación Curso de Actualización en la Enseñanza de la Matemática para Inspectores de
Educación Primaria. PMEM – ANEP. Montevideo.
• González Cabillón, J. – Lois, L. (1996) Matemática 4º. Ediciones de la plaza. Montevideo.
• Guías de Apoyo al Docente de Educación Secundaria - CBU.
• Hefez, A. (2006) Elementos de Aritmética. SBM. Río de Jeneiro.
• Lages Lima, E. y otros. (2004) A Matemática do Ensino Médio. Volume 1. SBM. Río de Janeiro.
• Lages Lima, E. y otros. (2004) Meu professor de Matemática e outras histórias. SBM. Río de
Jeneiro.
• Ochoviet, C. – Olave, M. (2006) Matemática 4. Ed. Santillana. Montevideo.
• Petracca, M. – Gilboy, A. (¿?) Geometría. Un poco de historia. Axiomas y definiciones.
• Puig Adam, Pedro; (1973) Geometría Métrica. Tomo I .Biblioteca Matemática. Madrid.
• Revistas do profesor de Matemática. Sociedad brasilera de Matemática. Río de Janeiro.
• Rodríguez Rava, B. – Xavier de Mello, M. (Comps.) (2005) El quehacer matemático en la escuela. Editorial
Queduca. Montevideo.
• Severi, Francisco (1965) - Elementos de Geometría. Editorial Labor. Barcelona.