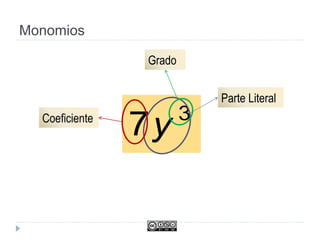
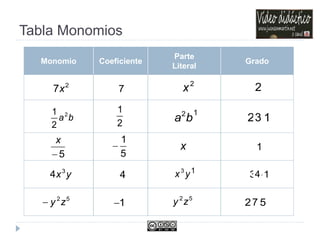
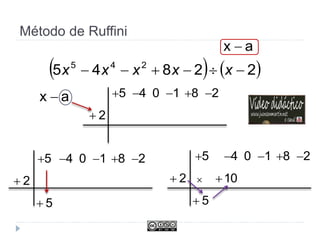
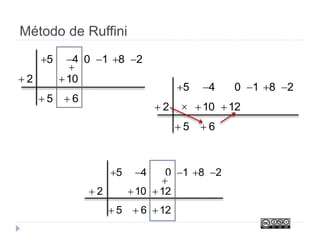
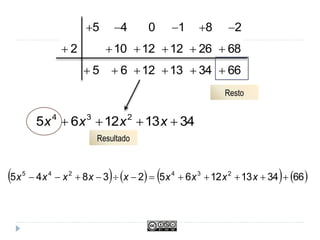
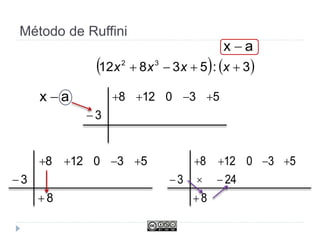
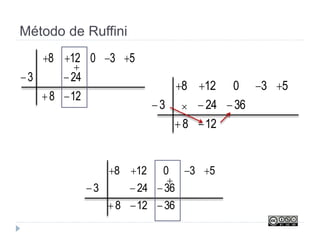
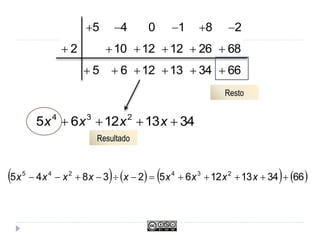
Este documento trata sobre polinomios. Explica conceptos como monomios, coeficientes, grado y operaciones con monomios. También cubre temas como identidades notables, el método de Ruffini para sumar polinomios, factorizar polinomios y trabajar con fracciones algebraicas.

1. Tema – Polinomios
Profesor Juan Sanmartín
Matemáticas
Recursos subvencionados por el…

2. Monomios
Parte Literal
3
7yCoeficiente
Grado

3. Tabla Monomios
Monomio Coeficiente
Parte
Literal
Grado
2
7x 7
2
x 2
ba2
2
1
2
1
ba2
12
1
3
5
x
5
1
 x 1
52
zy 1
52
zy 527
yx3
4 yx3
4 13 41

4. Operaciones con Monomios
22
53 xx 
xxxx 2727 22

333
3710 xxx 
xyyxxyyx 9494 22

53232
202054 xxxx  
    53322
b8ab4a2ab 
437
3
7
33
2
6
xx
x
x
 
2
8x
xxxx 2727 22


5. Identidades notables - Teoría
 2
ax ax2ax 22
  2
3x 3x23x 22
 9x6x2

ax2ax 22
 2
ax   2
7x 7x27x 22
 49x14x2

22
ax    axax     44x  x 22
4x  16x2

   baybay    22
bay 
 22
bax      bax2bax 2222
 2242
abxbxa 
 22
bxy      bxy2bxy 2222
 2224
bxy2xby 
222
bya 
CUADRADO DE LA SUMA Ejemplo
Ejemplo
CUADRADO DE LA DIFERENCIA Ejemplo
Ejemplo
SUMA POR DIFERENCIA Ejemplo
Ejemplo

6. Desarrolla las siguientes identidades notables:
a)
b)
c)
d)
e)
f)
Identidades notables
 2
5x 5x25x 22
 25x10x2

2
b
3
x






 b
3
x
2b
3
x 2
2







   yxzxyxzx     22
yxzx 
   23x23x    22
23x 
2
3
y
2
x






 
























3
y
2
x
2
3
y
2
x
22
 2
4x2      4x224x2
22
 16x16x4 2

222
2x3  4x9 2

3
2bx
b
9
x 2
2

6
2xy
9
y
4
x 22

3
xy
9
y
4
x 22

2222
xyxz   222
yzx 

7. Polinomios (Suma de monomios)
38745 2345
 xxxxx

8. Método de Ruffini
   22845 245
 xxxxx
ax 
2
281045


5
2
281045



5
102
281045



ax 


9. Método de Ruffini
65
102
281045



65
12102
281045



1265
12102
281045







10. 6634131265
68261212102
281045



34131265 234
 xxxx
Resultado
Resto
       663413126523845 234245
 xxxxxxxxx

11. 8
3
530128



Método de Ruffini
ax 
3
530128

ax 

   3:53812 32
 xxxx
8
243
530128




12. Método de Ruffini



128
243
530128



128
36243
530128



36128
36243
530128




13. 6634131265
68261212102
281045



34131265 234
 xxxx
Resultado
Resto
       663413126523845 234245
 xxxxxxxxx

14. Factorizar polinomios
01213 234
 xxxx
Paso 1.- Descomponemos la ecuación en factores.
041
1233
01211
12111
0121121
1211211
1211311







     043111213 234
 xxxxxxxx
Aplicamos RUFFINI para
factorizar la ecuación

15. Paso 2.- Obtenemos los factores e igualamos a cero..
    












04
03
01
01
04311
x
x
x
x
xxxx
404
303
101
101
4
3
2
1




xx
xx
xx
xx
Solución

16. Fracciones Algebraicas
16
1
4
3
4 2




 xxx
x
  
   164x4xm.c.m.
4x4x16x
4x4x
4x4x
2
2









x
   
  




4x4x
1434 xxx
  4x4x
112342



xxx
16
137
2
2



x
xx

17. Fracciones Algebraicas
2
1
442



 x
x
xx
x
   2
22
2m.c.m.
22
244x







x
xx
xx
  
 



 2
2
21
x
xxx
 
 2
2
2
22



x
xxxx
44
22
2
2



xx
xx
 



 2
2
2
22
x
xxxx

18. Fracciones Algebraicas
4
5
2
11
2



xxx
x
 42m.c.m.
44
22 2
22









xx
xx
xx
xx
    
 




42
254412
2
2
xx
xxxxx
 42
1048282
2
222



xx
xxxxxx
 42
8147
2
2



xx
xx

19. Fin de Tema
Busca enlaces a otras páginas relacionadas con
el tema en…
www.juansanmartin.net