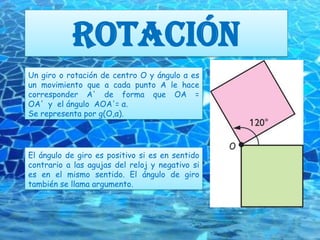
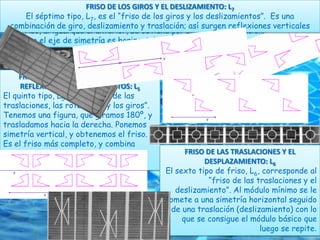
Este documento describe diferentes tipos de movimientos geométricos como traslaciones, giros, simetrías y sus aplicaciones en frisos y mosaicos. Explica que los frisos se forman mediante la aplicación repetida de traslaciones, giros, simetrías axiales y deslizamientos a figuras base. También describe siete tipos de frisos (L1-L7) y define los mosaicos como conjuntos de figuras que recubren el plano mediante traslaciones sin superposición ni huecos.

1. Movimientos en el PlanoPor el grupo 2:A.TN.E.YL.P.GA.L

2. Vamos a hablar de:·Las translaciones·Los giros·Las simetrías·Los frisos·Los mosaicos

3. DefiniciónUna transformación geométrica es una relación que hace corresponder a cada punto P del plano otro punto P' del plano. Se dice que P y P' son homólogos por la transformación. Los puntos que quedan transformados en ellos mismos se dice que son invariantes o puntos dobles.Un movimiento o isometría es una transformación en el que todas las figuras mantienen su forma y su tamaño. La distancia entre dos puntos cualesquiera de la figura se mantiene constanteLos movimientos pueden ser de dos tipos:Directos: Cuando el movimiento conserva el sentido, es decir, si el punto A se transforma en A’, el B en B’ y el C en C’ y al hacer el recorrido de estos puntos en el orden ABC se va en el sentido de las agujas del reloj. O sea, conserva la orientación de las figuras. Son movimientos directos la traslación, el giro o rotación y la simetría central. Inversos: Cuando el movimiento cambia el sentido, es decir, cuando se va en sentido contrario a las agujas del reloj. O sea, invierten la orientación.Es un movimiento inverso la simetría axial o reflexión.

4. TRASLACIÓNUna traslación de vector v es un movimiento directo en el plano que asocia a cada punto A un punto A' de forma que el vector AA’ es un vector de igual módulo dirección y sentido que v

5. RotaciónUn giro o rotación de centro O y ángulo α es un movimiento que a cada punto A le hace corresponder A' de forma que OA = OA' y el ángulo AOA'= α.Se representa por g(O,α).El ángulo de giro es positivo si es en sentido contrario a las agujas del reloj y negativo si es en el mismo sentido. El ángulo de giro también se llama argumento.

6. Simetría centralUna simetría central, de centro el punto O, es un movimiento del plano con el que a cada punto P del plano le hace corresponder otro punto P', siendo O el punto medio del segmento de extremos P y P'. Coordenadas mediante una simetría de centro O(0,0) :Un punto P' homólogo de un punto P(x,y) mediante una simetría central de centro O(0,0) tiene de coordenadas:Una simetría de centro O equivale a un giro de centro O y amplitud 180°.

7. Simetría AxialIgual ocurre con las figuras: a. Los segmentos CC’, BB’ y AA’ son perpendiculares a e. b. Los puntos C y C', B y B’, A y A’ equidistan del eje e. Dicho de otra forma el eje e es la mediatriz del segmento PP'Las simetrías axiales son isometrías porque conservan las distancias entre los puntos y sus homólogos.DEFINICIÓN: Dada una recta e se llama simetría axial de eje e al movimiento que transforma un punto A otro punto A’ verificando:Coordenadas de puntos mediante simetrías axialesCoordenadas de un punto simétrico al eje de ordenadasP(-x, y) x = -x' y = y' 1. El segmento AA' es perpendicular a e.2. Los puntos A y A' equidistan del eje e.3. Dicho de otra forma el eje e es la mediatriz del segmento AA'Al punto A’ se llama homólogo de A.Una simetría axial de eje “e” es una transformación, por tanto a todo punto P del plano le corresponde otro punto P' también del plano, de manera que el eje e sea la mediatriz del segmento AA'.Dos puntos A(x, y) y A'(x', y') simétricos respecto del eje de ordenadas tienen sus abscisas opuestas y sus ordenadas iguales.P(x, y)

8. Coordenadas de un punto simétrico al eje de abscisasDos puntos A(x, y) y A'(x', y') simétricos respecto del eje de abscisas tienen sus abscisas iguales y sus ordenadas opuestas.P(x, y) La composición de dos simetrías de ejes perpendiculares e y e' es una simetría central respecto del punto de corte de los dos ejes de simetría.Eje de simetríaP(x, -y) ---- x = x' y = -y' Composición de simetrías axialesSimetría de ejes paralelosLa composición de dos simetrías ejes paralelos e y e' es una traslación, cuyo vector tiene:- La longitud del vector es el doble de la distancia entre los ejes.- La dirección del vector es perpendicular a los ejes.- El sentido es el que va de e a e'. Simetría de ejes perpendicularesEl eje de simetría de una figura es la recta que divide a la figura en dos partes iguales, de modo que define una simetría axial entre una parte y otra.

9. EJEMPLOS DE SIMETRÍA

10. FRISOSEn primer lugar sepamos lo que el Diccionario de la Real Academia de la Lengua Española dice que es un friso:” Faja más o menos ancha que suele pintarse en la parte inferior de las paredes, de diverso color que estas. También puede ser de seda, estera de junco, papel pintado, azulejos, mármol, etc”. Es pues, lo mismo que una cenefa. Si nos fijamos, a nuestro alrededor los frisos están presentes de forma decorativa en muchas cosas. A continuación vamos a ver cómo las matemáticas están detrás de los procesos de formación de los frisos ya que se obtienen a partir de la aplicación de movimientos en el plano a una determinada figura o agrupación de figuras. Hay cuatro tipos de movimientos en el plano que intervienen en los frisos: la traslación, el giro, la simetría axial y el deslizamiento (el deslizamiento es la composición de una simetría axial y de una traslación). Jaime, A. y Gutiérrez, A. (1996) dicen en su libro lo siguiente: “Se llama friso a un cubrimiento de la región del espacio limitada por dos rectas paralelas. Los frisos son cubrimientos de regiones de longitud infinita pero de anchura finita.” Y nos indican cuáles son los movimientos en el plano que pueden formar parte de un friso: “- Las traslaciones de vector paralelo a los bordes de la región.Los giros de 180º cuyo centro equidista de los bordes de la región”Las simetrías cuyo eje es la recta que equidista de los bordes de la región o es perpendicular a dicha recta.Las simetrías en deslizamiento cuyo eje es la recta que equidista de los bordes de la región.

11. Algoritmo de Rose-Stafford

12. FRISO DE LAS TRASLACIONES L1El tipo L1 es el más simple, y se le suele llamar “friso de las traslaciones”, puesto que una determinada figura se traslada hacia la derecha varias veces, sin ninguna otra transformaciónFRISO DE LAS TRASLACIONES Y LAS ROTACIONES : L2El segundo tipo, L2, es el “friso de las traslaciones y las rotaciones”. Para generar este tipo de friso partimos de una figura, que giramos 180º, y luego trasladamos hacia la derechaFRISO DE LAS TRASLACIONES Y LAS REFLEXIONES VERTICALES: L3El tipo L3 es el “friso de las traslaciones y las reflexiones verticales”. Dibujamos una figura, y, a su derecha, trazamos un eje vertical, que utilizaremos como eje de simetría. Dibujamos la figura simétrica y trasladamos ambas figuras. Este friso se puede denominar “friso de simetría vertical”.

13. FRISO DE LOS GIROS Y EL DESLIZAMIENTO: L7El séptimo tipo, L7, es el “friso de los giros y los deslizamientos”. Es una combinación de giro, deslizamiento y traslación; así surgen reflexiones verticalesFRISO DE LAS TRASLACIONES Y LAS REFLEXIONES HORIZONTALES: L4El tipo L4 es el “friso de las traslaciones y la reflexión horizontal”. Este friso, al igual que el anterior, se obtiene por simetría y traslación. En este caso el eje de simetría es horizontal.FRISO DE LAS TRASLACIONES, GIROS, REFLEXIONES Y DESLIZAMIENTOS: L5El quinto tipo, L5, es el “friso de las traslaciones, las rotaciones y los giros”. Tenemos una figura, que giramos 180º, y trasladamos hacia la derecha. Ponemos simetría vertical, y obtenemos el friso. Es el friso más completo, y combina traslaciones, giros, reflexiones y deslizamientos.FRISO DE LAS TRASLACIONES Y EL DESPLAZAMIENTO: L6El sexto tipo de friso, L6, corresponde al “friso de las traslaciones y el deslizamiento”. Al módulo mínimo se le somete a una simetría horizontal seguido de una traslación (deslizamiento) con lo que se consigue el módulo básico que luego se repite.

14. MosaicosUn mosaico está formado por un conjunto de figuras que recubren el plano mediante traslaciones. Han de cumplirse dos condiciones:No pueden superponerse.

15. No pueden dejar huecos sin recubrir.Un mosaico se llama regular si está generado por un polígono regularLos únicos polígonos regulares que cubren el plano son el triángulo, el cuadrado y el hexágono

16. Un mosaico se llama semirregular si está compuesto por dos o más polígonos regulares.

17. Escher

18. Alhambra

19. Alhambra