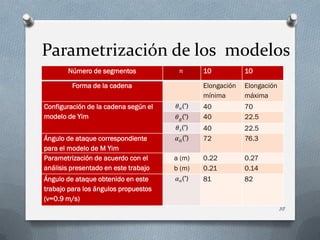
Este documento resume investigaciones previas sobre robots modulares y cadenas articuladas cerradas. Propone el desarrollo de un robot móvil modular con una cadena articulada cerrada que se mueva mediante rodadura. Describe los modelos cinemáticos y dinámicos requeridos para analizar el movimiento de la cadena, incluyendo parámetros como el ángulo de ataque, la elongación y la velocidad. El objetivo es explorar terrenos irregulares de forma eficiente y flexible.

1. Modular Snake
Robots
Robots Modulares
Ing. Kamilo Melo B., M.Sc
Ing. Alexandra Velasco Vivas, M.Sc.

2. Locomoción
O Locomoción en terrenos irregulares
O Mecanismos de locomoción convencionales

3. Antecedentes
O 1994. M. Yim et al. Nuevas formas de
locomoción
O 2000. M. Yim et al. PolyBot: a Modular
Reconfigurable Robot..
http://www.youtube.com/watch?v=02TCGo
1zyq8&feature=related

4. Antecedentes
O 2006. Locomoción de una cadena articulada
cerrada
O 2006. Robot modular deformable: Crawling and
Jumping.
O 2008. Análisis de Locomoción: Rolling Disk
Biped Hybrid Robot.
O 2008. Robot modular cerrado: Dynamic Rolling.
O http://www.youtube.com/watch?v=eOX6W2kFiE
c&feature=related

5. Cadena articulada cerrada
O Robot modular
O Propuesta: cadena
cerrada
O Ventajas: velocidad,
fluidez en el
movimiento, se detiene
rápidamente
Takeshi Matsuda, Satoshi Murata. Stiffness Distribution
Control, Locomotion of Closed Link Robot with
Mechanical Softness, Proceedings of the 2006 IEEE
International Conference on Robotics and Automation

6. Robot modular deformable
O Alternativa: robot deformable
Yuuta Sugiyama and Shinichi Hirai. Crawling and Jumping by a
Deformable Robot. The International Journal of Robotics
Research 2006; 25; 603

7. Rolling Disk Biped Hybrid Robot
O Modos de locomoción considerados: Escalar, caminar, rodar
Cristian C. Phipps, Benjamin E. Shores, and Mark A. Minor. Design and Quasi-Static Locomotion
Analysis of the Rolling Disk Biped Hybrid Robot. IEEE TRANSACTIONS ON ROBOTICS, VOL. 24, NO.
6, DECEMBER 2008

8. Rolling Disk Biped Hybrid Robot

9. Rolling Disk Biped Hybrid Robot

10. O
Yim CKBot
Robots modulares reconfigurables:
configuraciones y formas de
movimiento (gaits) para realizar
distintas tareas.
O Movimiento rodante: alta velocidad y
eficiencia
O Controlador: con base en sensores
para que el robot modular cerrado
ejecute un movimiento rodante
dinámico (dynamic rolling).
Jimmy Sastra, Sachin Chitta and Mark Yim, Dynamic
Rolling for a Modular Loop Robot. The International Journal
of Robotics Research 2009; 28; 758
http://www.youtube.com/watch?v=MoHW1L
aHsRQ

11. Movimiento rodante
Cinemático Dinámico

12. Movimiento Rodante
Dinámico
O Posición del centro de masas

13. Movimiento Rodante
Dinámico

14. Resistencia específica

15. O http://www.youtube.com/watch?v=VL0aiQA
m4RU
O http://www.youtube.com/watch?v=hj546C9
LR_o&feature=related

16. Motivación
O Exploración de entornos con terrenos
riesgosos o desconocidos.
O Locomoción de robots móviles en
terrenos no estructurados
O Cadenas articuladas
16

17. Nuestra propuesta: Robot
móvil
O Movimiento
O Representación de la cinemática y de la
Dinámica
O Ángulos de las junturas de los segmentos de la
cadena articulada
O Desempeño
17

18. CADENA ARTICULADA
O Junturas
O Locomoción
O Actuadores
O Configuración
18

19. CINEMÁTICA
O Movimiento
O Geometría
O Cinemática directa
O Cinemática inversa
O Centro de masa
19

20. DH
Juntura Parámetros DH para un módulo
1 0
2 0
3 0
i-1 0
i 0

21. Problema
O La obtención del modelo:
O Ecuaciones
O Soluciones
O Cinemática directa e inversa

22. Alternativas
O Modelos físicos:
O Lagrange
O Newton
O Otros
O Geometría

23. Marcos de referencia
O Marco mundo:
O Inercial
O Fijo
O Marcos de referencia de los
segmentos
O Marco de referencia del centro de
masa
23

24. Forma general de la cadena
0.4
0.35
0.3
yCM
0.25
CM
0.2 xCM
0.15
0.1
yw
0.05
xw 24
0
-0.3 -0.25 -0.2 -0.15 -0.1 -0.05 0 0.05 0.1 0.15

25. Centro de masa
25

26. DINÁMICA
O Aproximación al péndulo invertido:
•Forma elipsoidal
•Dinámicamente inestable: péndulo
invertido.
•Ángulo de inclinación con respecto al
eje vertical: tiende a caer.
•En este caso no se tiene un elemento
para desplazamiento en el eje
horizontal (carrito)
cae
O Principio para rodar: evitar que la
cadena caiga
Movimiento en x
26

27. DINÁMICA
O Geometría: Elipse continua
O Ángulo de ataque
O Centro de masa
O Restricciones
αattack
27

28. Casos de análisis: elipse
Caso 1 Caso 2
28

29. Diagrama de cuerpo libre
29

30. DINÁMICA
30

31. Fuerzas
31

32. Torques
32

33. Ecuaciones
33

34. Ángulos de juntura a partir de
la velocidad
O Para programar el movimiento deseado de
una cadena de n segmentos, a partir de una
velocidad establecida, se requiere:
• Curva de velocidad
• Elongación de la cadena
• Ángulo de ataque
• Valores de a y de b de la elipse
• Valores de los ángulos de las junturas
• Corrimiento de los ángulos de las junturas
34

35. Velocidad lineal y Aceleración
lineal
3 intervalos: aceleración, crucero y desaceleración
v(t) (m/s)
Crucero
t (s)
35
t0 tf tf +t0

36. Ángulos de ataque
1. Modelo del péndulo invertido
2. Control de la posición angular del eje mayor de la
cadena articulada cerrada
7. Se encuentran todos los ángulos de ataque posibles
para tener la máxima velocidad lineal establecida.
36

37. Parámetros utilizados en el
modelo de M.Yim
O Ángulo apex θa.
O El resto de ángulos de
juntura de la cadena son
iguales entre sí
O 2 + ( − 2) = 2,
O es el ángulo de
inclinación de la cadena

38. Parametrización de los modelos
Número de segmentos 10 10
Forma de la cadena Elongación Elongación
mínima máxima
Configuración de la cadena según el 40 70
modelo de Yim 40 22.5
40 22.5
Ángulo de ataque correspondiente 72 76.3
para el modelo de M Yim
Parametrización de acuerdo con el a (m) 0.22 0.27
análisis presentado en este trabajo b (m) 0.21 0.14
Ángulo de ataque obtenido en este 81 82
trabajo para los ángulos propuestos
(v=0.9 m/s)
38

39. Resultados
Número de segmentos: 10
Masa de cada segmento= 0.138 kg
Longitud de cada segmento = 0.06 m
Velocidad terminal: 1.6 m/s para una elongación máxima
Máxima elongación: 24 cm
n=10 Velocidad crucero Ángulo de
segmentos (terminal) ataque
Modelo M. 1.6 m/s 76.3°
Yim
En el modelo 1.6 m/s 78°
presentado 1.8 m/s 76.3°
Error % en el ángulo de ataque= 2.2%
39

40. Consideraciones mecánicas
O Una cadena articulada cerrada tiene
O n links conectados por n junturas
O Módulos:
O Un grado de libertad por cada juntura.
O El número de módulos está determinado
por:
O Torque nominal de cada servomotor
O Configuración de la cadena

41. Los segmentos
41

42. EJEMPLO
O Velocidad crucero: 0.45 m/s
O Tiempo: 20 unidades (T=0.3 s).
O n=10 segmentos
O Mínima elongación posible para la
cadena de n=10
O La aceleración y la desaceleración
pueden tener una pendiente constante
que depende de la velocidad angular de
los motores.
42

43. Curva de velocidad
0.45
Velocidad [m/s]
2 4 6 8 10 12 14 16 18 20
Tiempo [unidades de T]
43

44. Resultados: ángulo de ataque
O Reposo:
O Ángulo de ataque de 90°
O Aceleración:
O Ángulo de ataque: entre 90° y 85.5°.
O Velocidad crucero:
O Ángulo constante: 85.5°
O Desaceleración:
O Ángulo de ataque: entre 85.5°y 90°
44

45. 90
Resultado: Ángulo de ataque
Ángulo de ataque [°]
86.5
2 4 6 8 10 12 14 16 18 20
Tiempo [unidades de T]
45

46. Q1
40
35
30
25
0 2 4 6 8 10 12 14 16 18 20
46

47. Q2
40
35
30
25
0 2 4 6 8 10 12 14 16 18 20
47

48. Q3
40
35
30
25
0 2 4 6 8 10 12 14 16 18 20
48

49. Q4
40
35
30
25
0 2 4 6 8 10 12 14 16 18 20
49

50. Q5
40
35
30
25
0 2 4 6 8 10 12 14 16 18 20
50

51. Q6
40
35
30
25
0 2 4 6 8 10 12 14 16 18 20
51

52. Q7
40
35
30
25
0 2 4 6 8 10 12 14 16 18 20
52

53. Q8
40
35
30
25
0 2 4 6 8 10 12 14 16 18 20
53

54. Q9
40
35
30
25
0 2 4 6 8 10 12 14 16 18 20
54

55. Q10
40
35
30
25
0 2 4 6 8 10 12 14 16 18 20
55

56. Cálculo de velocidades

57. t1: Movimiento
0.6
0.5
0.4
0.3
0.2
0.1
0
-0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3
57

58. t2: Movimiento
0.6
0.5
0.4
0.3
0.2
0.1
0
-0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3
58

59. t3: Movimiento
0.6
0.5
0.4
0.3
0.2
0.1
0
-0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3
59

60. t4: Movimiento
0.6
0.5
0.4
0.3
0.2
0.1
0
-0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3
60

61. t5: Movimiento
0.6
0.5
0.4
0.3
0.2
0.1
0
-0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3
61

62. t6: Movimiento
0.6
0.5
0.4
0.3
0.2
0.1
0
-0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3
62

63. Centro de masa
O Representación del movimiento
O Se calcula el centro de masa de la
cadena articulada cerrada en el
tiempo
O A partir de los ángulos de las junturas
de la cadena articulada cerrada en el
tiempo
63

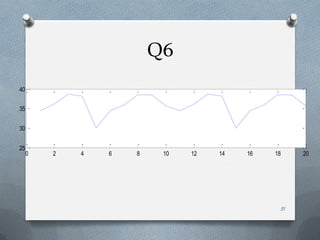
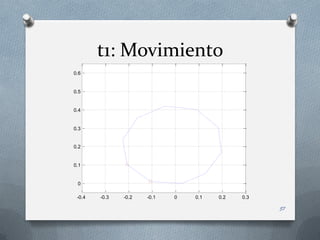
64. Centro de masa: x a=0.22 m, b=0.21 m
3
2.5
2
Distancia [m]
1.5
1
0.5
0
0 2 4 6 8 10 12 14 16 18 20
Tiempo [unidades de t]64

65. Centro de masa: y a=0.22 m, b=0.21 m
0.225
0.22
0.215
Distancia [m]
0.21
0.205
0.2
0.195
0.19
0 2 4 6 8 10 12 14 16 18 20
Tiempo [unidades de t]65

66. Centro de masa
1
0.8
0.6
0.4
0.2
y [m]
0
-0.2
-0.4
-0.6
-0.8
-1
1
0.8
0.6
0.4 0
0.2 0.5
0 1
-0.2 1.5
-0.4
-0.6 2
-0.8 2.5
-1 3
x [m]
z [m] 66

67. 1.6
Resultados
Velocidad [m/s]
2 4 6 8 10 12 14 16 18 20
Tiempo [unidades de T] 67

68. Resultados
90
Ángulo de ataque [°]
78
2 4 6 8 10 12 14 16 18 20
Tiempo [unidades de T] 68

69. Curva de velocidad
O n=10; v=0.9 m/s; elongación máxima
0.9
Velocidad [m/s]
2 4 6 8 10 12 14 16 18 20
69
Tiempo [unidades de T]

70. Ángulo de ataque: 79,3°
90
Ángulo de ataque [°]
80
2 4 6 8 10 12 14 16 18 20
70
Tiempo [unidades de T]

71. MÉTRICAS
8 10 14
m [kg] 0.88 1.1 1.54
v [m/s] 0.9 > 0.9 > 0.9
P [W] 86.4 108 146.2
5.6 <5.6 <5.6
Ángulo [°] 45 < 45 <45
η
71

72. Otros robots modulares
O http://www.youtube.com/watch?v=v6W-
sEpJEqY
O http://www.youtube.com/watch?v=4kFpG_x
fymghttp://www.youtube.com/watch?v=H89
Tte4LCVc&feature=related
O http://www.youtube.com/watch?v=68mp7d
YUOWU