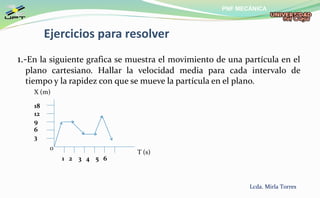
El documento presenta información sobre el movimiento de partículas en el plano. Explica que existen diferentes tipos de movimiento como el rectilíneo uniforme, acelerado y retardado. También describe el movimiento circular, la caída libre y el movimiento oblicuo de una partícula. Incluye fórmulas para calcular la velocidad, aceleración, posición y otros parámetros del movimiento. Además, contiene ejemplos resueltos para demostrar el cálculo de estas variables en diferentes situaciones cinemáticas.

1. Trayectoria
C
B
Trayectoria desde A
hasta D
Punto de Referencia
Posición B
Unida III. CINEMATICA DE PARTICULAS
D
Facilitador : Lcda. Mirla Torres
PNF MECÁNICA
Abril 2021
Determinar el vector velocidad y
aceleración que describa el movimiento
de una partícula en el plano.
Objetivo:
A

2.  Movimiento rectilíneo uniforme: Cuando su velocidad es constante
entonces hablamos de , para el calcula de la velocidad media
se tiene entonces que
 Movimiento rectilíneo uniforme variado: Acelerado y Retardado
 Movimiento circulares curvilíneos, elípticos, parabólicos, Helicoidal
V= X/t
V m= X 2 – X 1 / t2- t1
Lcda. Mirla Torres
Unida III. CINEMATICA DE PARTICULAS
PNF MECÁNICA
Movimiento de una partícula en el plano

3. Movimiento de una partícula en el Plano
Cinemática en una dimensión.
 Movimiento sobre una recta.
El movimiento de una partícula que se mueve sobre una recta lo podemos describir de
la siguiente manera:
Donde: el punto O es la referencia con relación a los puntos A y B , este
movimiento de la partícula a lo largo de la recta se denomina movimiento
rectilíneo uniforme .
0
-1
-2 1
-3 2 3
A B
O
X Vector posición
PNF MECÁNICA
Lcda. Mirla Torres

4. Un cuerpo se mueve de acuerdo a la ecuación X=3t²-7t+2 determinar:
a ) Posición de la partícula para un t= 1s , T=2s T=3s
b) La velocidad media para t= 3s y t= 5s
Solución
a ) se tiene
 Para T=1 en la ecuación X=3(1)²-7(1)+2 = -2 m
 Para T=2 en la ecuación X=3(2)²-7(2)+2 = 0m
 Para T=3 en la ecuación X=3(3)²-7(3)+2 = 8 m
X= X3- X 1 = 8-(-2)m ;
X=10m
b) Velocidad Media seria:
O
-1
-2 8
. . .
V m= X m – X 1/ t5- t3
V= 8m – (-2m) = 5m/s
5s - 3s
EJEMPLO
PNF MECÁNICA
Lcda. Mirla Torres

5. Ejemplos
La siguiente tabla muestra los datos que se obtienen al medir las diferentes
posiciones que ocupa una partícula en diferentes intervalos de tiempo dados .
¿Calcular la velocidad ?
X (m) 0 40 80 120 160
T (s) 0 4 8 12 16
X (m)
T (s)
160
120
80
40
0
0 4 8 12 16
40m/4s =10m/s
80m/8s =10m/s
120m/12s =10m/s
160m/16s = 10m/s
V= 160m – 40m = 10 m/s
16s - 4s
V= X/t ; V= 160m = 10m/s
16 s
V m= ∆X = X 2 – X 1 / t2- t1
∆t
Desplazamientos X
∆X= X2-X1 ; ∆X =160m-0m=160
∆t= t2-t1 ; ∆t=16seg – 0seg= 16seg
PNF MECÁNICA
Lcda. Mirla Torres

6. Ejercicios para resolver
1.-En la siguiente grafica se muestra el movimiento de una partícula en el
plano cartesiano. Hallar la velocidad media para cada intervalo de
tiempo y la rapidez con que se mueve la partícula en el plano.
X (m)
T (s)
18
12
9
6
3
0
1 2 3 4 5 6
PNF MECÁNICA
Lcda. Mirla Torres

7. 2.)Un cuerpo se desplaza de modo que su posición en función del tiempo esta dado por la
grafica de la fig. hallar la rapidez con que se mueve y la velocidad de la partícula.
80
40
T (s)
X (m)
5 10
0
Ejercicios para resolver
PNF MECÁNICA
Lcda. Mirla Torres

8. Movimiento de una partícula en el Plano
PNF MECÁNICA
Lcda. Mirla Torres
Aceleración media e instantánea: es el cambio de la velocidad en cada
unidad de tiempo, se trata de una magnitud vectorial.
La aceleración media viene dada por :
Y la aceleración instantánea viene dada por: a =Vf-V0 si el móvil parte
del reposo se tiene t- t0
a med = V2 –V1 = ∆V
t2 - t1 ∆ t
a = Vf = m /s.
t
Si el movimiento se da con aceleración constante se deduce que :
1 ) V= V0 + at
3 ) X = X0 + V0 T + ½ at² ; X= ½ at²
2 ) Vf ² = V0 ² + 2ax MUA ; V ² = V0 ² - 2a (x-X0) MUR (movimiento uniforme retardado)
4) X máx.= -V0²
2a
5) T máx.= Vo
a

9. Ejemplo
1) Calcular la rapidez con la cual se desplaza un móvil que al cabo
de 30s. de estarse moviendo con una aceleración de 0,5m/s² de
tiene rapidez de 18m/s.
Solución: extraemos los datos y aplicamos la formula V=V0+at
Datos V= V0 + at
T=30 s.
VF=18m/s V0 = 18m/s - 0.5m/seg² . 30 s
a=0,5m7s² V0=3m/ s
PNF MECÁNICA
Lcda. Mirla Torres

10. 2) Un móvil que se desplaza a 60Km/s. Se le aplican los frenos durante 5min.
Teniendo al final de la frenada una rapidez de 15km/h. Calcular la
aceleración del móvil.
Datos:
Vo=60Km/h 60k/h . 1000m/3600s =16,67m/s
T= 0,5min 0,5 min . 60s = 30s
Vf= 15Km/h 15Km/h . 1000m/3600s = 4,16m/s
a = Vf –V0 ; a = 4,16m/s –16,67m/s
t 30s.
a = - 0,4m/s²
Ejemplo
PNF MECÁNICA
Lcda. Mirla Torres

11. Ejercicios para resolver
 Un móvil parte del reposo iniciando un movimiento uniforme
acelerado(MUA) con una aceleración de 1,2m/s² la cual mantiene
durante 20 s. Calcular la rapidez que tendrá al final de ese tiempo?
 Calcular el tiempo que tarda un móvil en variar su rapidez desde 8m/s
hasta 15m/s sabiendo que su aceleración constante es de 0,7 m/s.
 En el momento de comenzar a contar la rapidez de un móvil, este tiene
60Km/h si mantiene una aceleración de 360m/s². Calcular la rapidez
que tendrá a los 30s de movimiento?
 Un móvil en un momento dado acelera a razón de 1,5m/s², la cual
mantiene durante 25s si al final de esta aceleración tiene una rapidez
de 100Km/h. Calcular la rapidez que tenia en el momento de comenzar
la aceleración?
PNF MECÁNICA
Lcda. Mirla Torres

12. Resumen de las formulas
a) a med = ∆V = Vf –V0 aceleración instantánea
∆ t t2 - t1
a = Vf = m /seg²
t
b)V= V0 + at
d ) X = V0. T + at² ; si parte del reposo V0=0 entonces X= 1 at² el
2 2
movimiento es acelerado, si X= V0. T - 1 at² el movimiento es retardado
2
c ) Vf ² = V0 ² + 2ax MUA ; Vf ² = V0 ² - 2ax MUR
e) X máx.= -V0²
2a
f)T máx.= - Vo
a
PNF MECÁNICA
Lcda. Mirla Torres

13. MOVIMIENTO DE UNA
PARTICULA EN EL
PLANO
PNF MECÁNICA
Universidad Politécnica
Territorial del Zulia
MOVIMIENTO CIRCULAR
Lcda. Mirla Torres
Cinemática de Partículas

14. Movimiento circular uniforme
 Elementos del movimiento
-Periodo T= t/n
-Movimiento periódico
-Frecuencia F= n/t
Cinemática
Movimiento de una partícula en el Plano
V
V
V
V
V
V
arad
arad
arad
arad
arad
arad
R
Velocidad angular ( ) ;
unidad es: rad/s
Velocidad angular en función de frecuencia
y periodo
Velocidad Lineal (V)
Aceleración radial o centrípeta (arad)
rad rad
rad
PNF MECÁNICA
Lcda. Mirla Torres

15.  Ejemplo : Un disco
de 9m de diámetro
está girando de
manera que da 15
vueltas en 0,5min.
calcular:
 a.) La velocidad lineal
 b.) La velocidad
angular
 c.) La frecuencia
 d.) La aceleración
radial o
centrípeta.
 e.) Cuantas vuelta da
en 1,5 minutos.
 f.) Cuanto tarda en
dar 80 vueltas.
Cinemática : Movimiento circular
Solución
Datos:
D=9m ;
R= 4,5m
n=15
t=0,5 min
0.5x60 s =30s
V= ?
V angular = ?
f = ?
arad =?
n= ? en 15 min
1,5x60s = 90s
t = ? En dar 80
n=80 vueltas
a)Velocidad lineal pero
luego
b)Velocidad angular
c) La frecuencia
d) La aceleración radial o centrípeta
e) Cuantas vuelta da en 1,5 minutos. Utilizando la
f.) Cuanto tarda en dar 80 vueltas.
V
V
V
V
V
V
Lcda. Mirla Torres

16. CINEMATICA DE PARTICULAS
 MOVIMIENTO VERTICAL : CAÍDA LIBRE
Ys=Y- Yl
Aceleración constante = g=9,8 m/seg²
(Ec. a) Vf = g.t
(Ec. b) Y= g.t²
2
(Ec. c) V²= 2 gY
Formulas:
Y
Yl=g.t²
2
Vf = g.t
Suelo
(Ec. d) Ys=Y- Yl
Lcda. Mirla Torres
PNF MECÁNICA
La caída libre: es el movimiento
adquirido por el cuerpo cuando
se deja caer en el vacio.
Este movimiento se da a lo
largo de la línea vertical y es
uniformemente acelerado

17.  Desde una altura de 80m se deja caer un cuerpo. Calcular a los 3seg:
a) La rapidez que tiene en ese momento. b) la altura a la cual se
encuentra del suelo
Solución
Datos:
Y=80m
t=3seg.
Vf= ?
Ys=?
g=9,8 m/seg²
Ejemplo
a) La rapidez que tiene en ese momento
Vf=g.t = 9,8 m/seg² . 3seg. = 29,4m/seg.
b) la altura a la cual se encuentra del suelo
(Ec. d) Ys=Y- Yl Yl =g.t² = 9,8 m/seg² . 9seg=45m
2
Sustituyendo Yl=45m y Y= 80m en (Ec. d)
Ys=80m - 45m
Ys=35m
CINEMATICA MOVIMIENTO VERTICAL
PNF MECÁNICA
Lcda. Mirla Torres

18. CAIDA LIBRE
 Desde una torre se deja caer una piedra que tarda 5 seg. en llegar al suelo. Calcular
la rapidez que tiene en ese momento. de la torre.
 Desde una altura de 20m. se deja caer un cuerpo. la rapidez que lleva a los 5seg. y la
altura a la cual se encuentra del suelo a los 5 seg.
 Desde una altura de 300m se deja caer un cuerpo pesado. Calcular el tiempo que
tarda en llegar al suelo y la rapidez que tiene en ese momento.
 Un cazador esta disparando contra una bandada de gaviotas, que vuelan a unos 50m
de altura. Una de las gaviotas cae herida y se desprende en caída libre de la manada.
a) ¿Qué distancia recorre el ave y que velocidad alcanza a t=1,2,3seg. b) Cuánto
tiempo y qué velocidad tiene la gaviota al chocar contra la superficie terrestre?
Ejercicios para resolver PNF MECÁNICA
Lcda. Mirla Torres

19. CINEMÁTICA : MOVIMIENTO DE PARTÍCULAS
y
V0=Vx
Vy
Vx
Vx
V
A
Vy
V
B
C
X
fig. 1
V0=Vx Vy= g. t V²= (Vx)² +(Vy)²
Tanᾳ = Vy
Vx
Desplazamiento (d)
X = Vo . t
Y =g.t²
2
d²= X² + Y² Tanᾳ = y
x
Tv= √ -2Y
g
Tv= Alcance
V0
X
y
y
Vx=V0
V0
V
X
Vy= - g .t
0
Para un t=0,5
X=V0 . t = (9.0m/ s) (0,50s) = 4,5 m
Y = - g.t² = ( 9,8m/s²)(0,50s)² = -1.2m
2 2
La distancia de la moto ahora es d=√X²+Y²
d=√ (4.5m)² + (-1,2m)² =4,7m
Las componentes de la velocidad en ese tiempo son= Vx=Vox =
9,0m/s ; Vy=- g. t =(9,8m/s²)(0,50)=-4,9m/s
El modulo de velocidad es V²= (Vx)² +(Vy)²
V=√ (9,0m/s)²+ (-4,9m/ s)² y la dirección Tanᾳ = Vy
Vx
ᾳ =arcTan Vy = (-49m/ s) = 29°
Vx (9,0m/ s)
V= √(Vx)² +(Vy)²

20. V
V0x=Vx
V
Vx
0
V y
V
a
fig. 2
Y
X
Vx
Vx
Vx
Vy
a
a
a
a
V0y
Vy
V
V
Vy=-Voy +gTv
. Vy=0
.
.
. .
R= Alcance
V0x= V0 . cosᾳ
V0y=V0. Senᾳ
Vx=V0x=Vo.cosᾳ .t
Vy=V0y +gt
V²= (V y)² +(Vx)²
Tanᾳ =V y ;
Vx
Tv= 2 Tmáx
TV=2 V0senᾳ
g
Tmáx= -V0y
g
Ymáx=-V0y²
2 g
X = (V0 . cosᾳ) t
R=Vox . Tv
Ymáx
ᾳ =arc Tan Vy
Vx
y=V0. Senᾳ.t+1gt²
2
Vy=0=V0y-gt
Vy=0=V0y-gt
t=V0y
g
h
h=y=V0yt1-1gt²
2
R =V0²sen(2ᾳ)
g
CINEMÁTICA : MOVIMIENTO DE PARTÍCULAS
PNF MECÁNICA

21. Ejemplo
 Se lanza un proyectil con una velocidad de
400m/s y un ángulo de elevación de 30°
calcular el alcance del proyectil
Solución:
V
V0x=Vx
V
Vx
0
V y
V
a
fig. 2
Y
X
Vx
Vx
Vx
Vy
a
a
a
a
V0y
Vy
V
V
Vy=-Voy +gTv
. Vy=0
.
.
. .
R= Alcance
V0x= V0 . cosᾳ
V0y=V0. Senᾳ
Vx=V0x=Vo.cosᾳ
Vy=V0y +gt
V²= (V y) +(Vx) ;
Tanᾳ =V y ;
Vx
Tv= 2 Tmáx
Tmáx= -V0y
g
Ymáx=-V0y²
2 g
X = (V0 . cosᾳ) t
R=Vox . Tv
Ymáx
ᾳ =arc Tan Vy
Vx
y=V0. Senᾳ.t+1gt²
2
R = 14139.19m
ᾳ
R=Vox . Tv sustituyendo
R=V0cosᾳ. 2V0sen ᾳ resolviendo
g
Solución
R =V0²sen(2ᾳ) =400².sen(2.30°)=400.sen(60°)
g 9,8m/seg² 9,8m/seg²
Voy
Vox=Vx
v
CINEMÁTICA : MOVIMIENTO DE PARTÍCULAS
PNF MECÁNICA

22. r(t)= x(t) i+ y(t) j +z(t) k
x
y
Z
k
i
j
X i
Y j
Z k
Desplazamiento y Velocidad
∆t 0. P1 r1
P2 r2
∆r= r2 - r1
∆r= r2-r1 = (x2-x1) i+ (y2-y1) j +(z2-z1t) k
Magnitud |∆r|=√∆x²+∆y² +∆z²
V med = ∆r = r2-r1 = ∆x i + ∆y j +∆z k
∆t t2-t1 ∆t ∆t ∆t
V = Lím ∆r = d r
∆t 0 ∆ t d t
x
Z
y
∆r
t1
t2
r1
r2
Ecuación Vectorial
= d x i + dy j + d z k
dt dt dt
Vector posición r(t0)
PNF MECÁNICA
Lcda. Mirla Torres
Cinemática en tres dimensión

23. Cinemática en tres dimensión
v = dr = d x i + dy j + d z k
dt dt dt dt
Las componentes del vector velocidad en las direcciones de los ejes coordenados son:
V x = dx Vy = dy Vz = dz
dt dt dt
y el módulo de la velocidad o celeridad es:
V = ds = √ Vx² +Vy² + Vz²
dt
PNF MECÁNICA
Lcda. Mirla Torres

24.  Aceleración
a med = Δv y la instantánea a = lím Δv = dv =v’
Δt Δt→0 Δt dt
en función del vector de posición a = d²r = r”
d²t
En coordenadas cartesianas con los versores cartesianos (i ,j, k)constantes,
se tiene:
a = dV = dVx i + dVy j + dVz k a = d²r = d²x i + d²yj + d²zk
dt dt dt dt dt² dt² dt² dt ²
Las componentes de la aceleración en las direcciones de los ejes coordenados
son: ax = dvx ay= dvy az= dvz entonces a x= d²x ay= d²y az= d²z
dt dt dt dt² dt² dt²
su módulo es a = √ ax²+ ay² + az²
Cinemática en tres dimensión