Este documento presenta información sobre el movimiento rectilíneo uniforme (MRU). Explica que en un MRU, la velocidad es constante y la aceleración es cero. Proporciona las ecuaciones cinemáticas para un MRU y describe cómo graficar la posición, velocidad y aceleración en función del tiempo para este tipo de movimiento. También analiza conceptos como desplazamiento, velocidad y distancia recorrida en problemas de MRU.

1. FÍSICA
1º de Bachillerato
2 009 – 2 010
Ing. EDGAR JACINTO ESPINOZA BERNAL
1

2. Hace unos 2 500 años, Confucio declaró:
Lo que escucho, lo olvido.
Lo que veo, lo recuerdo.
Lo que hago, lo comprendo
2

3. CREDO DEL APRENDIZAJE ACTIVO:
•Lo que escucho, lo olvido.
•Lo que escucho y veo, lo recuerdo un poco.
•Lo que escucho, veo y pregunto o converso con otra
persona, comienzo a comprenderlo.
•Lo que escucho, veo, converso y hago, me permite
adquirir conocimientos y aptitudes.
•Lo que enseño a otro lo domino.
Para aprender algo bien conviene:
Escucharlo, verlo, formular preguntas al respecto y
conversarlo con otros.
Los estudiantes necesitan “hacerlo”, descubrir las cosas
por su cuenta.
3

4. CLASIFICACIÓN DEL MOVIMIENTO
Según la TRAYECTORIA
Una línea recta: horizontal,
RECTILINEO
vertical, inclinada
CIRCULAR Una circunferencia
Una línea curva: parábola,
CURVILINEO
elipse
4

5. CLASIFICACIÓN DEL MOVIMIENTO
Según la VELOCIDAD
UNIFORME Velocidad constante
UNIFORMEMENTE Velocidad cambia
ACELERADO uniformemente
VARIADO Velocidad variable
5

6. CLASIFICACIÓN DEL MOVIMIENTO
Según la ACELERACIÓN
UNIFORME Aceleración es cero
UNIFORMEMENTE
Aceleración constante
ACELERADO
VARIADO Aceleración variable
6

7. CLASIFICACIÓN DEL MOVIMIENTO
Estos movimientos por sí solos no existen en la naturaleza,
son el resultado de combinar la clasificación anterior, así
tendremos:
Movimiento Rectilíneo Uniforme: MRU
Movimiento Rectilíneo Uniformemente Acelerado: MRUA
Movimiento Circular Uniforme: MCU
Movimiento Circular Uniformemente Acelerado: MCUA
En este capítulo aprenderemos a describir
EL MOVIMIENTO RECTILÍNEO EN UNA DIMENSIÓN.
7

8. MOVIMIENTO RECTILÍNEO
Se clasifica en:
Movimiento Si la velocidad es constante (v = cte)
Rectilíneo Entonces, la aceleración es cero
Uniforme (a = 0)
Movimiento
Si la velocidad varía uniformemente
Rectilíneo
Entonces, la aceleración es
Uniformemente
constante (a = cte)
Acelerado
8

9. MOVIMIENTO RECTILÍNEO
Todo movimiento se define por una de sus ecuaciones
cinemáticas, nuestra tarea es deducir las otras dos por
medio de las definiciones de posición, velocidad y
aceleración.
ECUACIONES CINEMÁTICAS
Posición en función del tiempo:
X = f (t)
Velocidad en función del tiempo:
V = f (t)
Aceleración en función del tiempo:
a = f (t) 9

10. Movimiento Rectilíneo Uniforme
MRU
Un móvil está animado de MRU cuando:
•La TRAYECTORIA que describe es una LÍNEA RECTA
•La VELOCIDAD permanece CONSTANTE
•Es decir, recorre distancias iguales en intervalos iguales de tiempo
0 1 2 3 4 5 t (h)
V=30 km/h
0 30 60 90 120 150 X (km)
Por ejemplo: el automóvil recorre 30 km (ΔX=30 km) en cada hora
(Δt=1 h). Es decir, se mueve con una velocidad de 30 km/h, la cual
permanece constante durante el movimiento. 10

11. Movimiento Rectilíneo Uniforme
MRU
La VELOCIDAD permanece CONSTANTE, significa que: los cambios
de posición (ΔX) respecto al tiempo (Δt) son UNIFORMES (o
CONSTANTES)
0 1 2 3 4 5 t (h)
V=30 km/h
0 30 60 90 120 150 X (km)
∆X ∆X X − X 0
= cte V= =
∆t ∆t t − t0 11

12. Movimiento Rectilíneo Uniforme
MRU
ECUACIONES CINEMÁTICAS
Posición X = X 0 + V ⋅ ∆t
∆X X − X 0
Velocidad V= =
∆t t − t0
Aceleración a=0
12

13. Gráficos del MRU
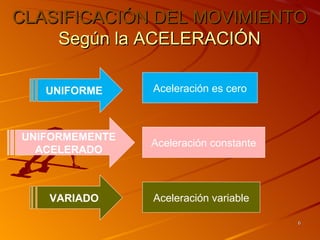
Si la aceleración es nula (a=0), la gráfica aceleración en
función del tiempo [a = f(t)] no existe.
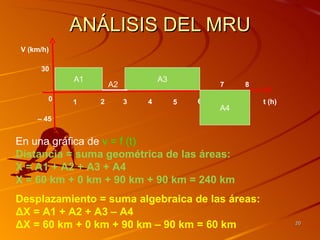
Si v = cte, la gráfica velocidad en función del tiempo [v = f(t)]
es una línea recta horizontal paralela al eje de los tiempos.
El área bajo esta línea,
representa la distancia
recorrida en el intervalo de
tiempo correspondiente.
13

14. Gráficos del MRU
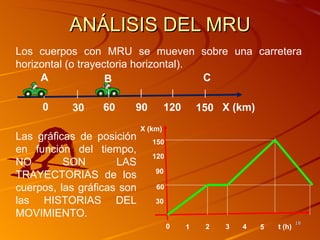
La gráfica posición en función del tiempo [X = f(t)] es una
línea recta inclinada que puede o no pasar por el origen.
X0 = 0 X0 ≠ 0
La pendiente de la recta ∆X X 2 − X 1
tan θ = V = =
representa a la velocidad. ∆t t 2 − t1 14

15. ANÁLISIS DEL MRU
En el desplazamiento:
Si xf > x0 entonces Δx > 0 (se mueve hacia la derecha)
Si xf < x0 entonces Δx < 0 (se mueve hacia la izquierda)
Si xf = x0 entonces Δx = 0 (está en reposo o regresó al
punto de partida)
La distancia recorrida por un cuerpo es el valor del módulo
del desplazamiento (siempre y cuando no exista un regreso
o cambio de dirección)
Ejemplo 1: un móvil parte de la posición X=5 m hacia la posición X=12 m,
determine el vector desplazamiento y la distancia recorrida.
∆X ∆X=X – X0
0 ∆X=12 m – 5 m
X0 =5 m X=12 m
d ∆X=7 m
d = |∆x| = |7 m| = 7 m
Respuesta: el desplazamiento del móvil es 7 m (hacia la derecha) y la
15
distancia recorrida es 7 m.

16. ANÁLISIS DEL MRU
Ejemplo 2: un automóvil parte de la posición X=–5 m hacia la posición
X=10 m, determine el vector desplazamiento y la distancia recorrida.
∆X ∆X=X – X0
X0 = – 5 m 0 X=10 m ∆X=10 m – (– 5 m)
d ∆X=15 m
d = |∆x| = |15 m| = 15 m
Respuesta: el automóvil se desplaza 15 m (hacia la derecha) y la
distancia que recorre es 15 m.
Ejemplo 3: un hombre parte de la posición X=8 m hacia la posición X=5 m,
determine el vector desplazamiento y la distancia recorrida.
∆X ∆X=X – X0
0 X=5 m X0 =8 m ∆X=5 m – 8 m
d ∆X= – 3 m
d = |∆x| = | – 3 m| = 3 m
Respuesta: el hombre se desplaza 3 m (hacia la izquierda) y la distancia 16
que recorre es 3 m.

17. ANÁLISIS DEL MRU
En la velocidad:
La velocidad media es igual a la velocidad instantánea
Si la velocidad es positiva el cuerpo se mueve hacia la
derecha
Si la velocidad es negativa el cuerpo se mueve hacia la
izquierda.
La rapidez es el valor del módulo de la velocidad (no
siempre)
17

18. ANÁLISIS DEL MRU
Los cuerpos con MRU se mueven sobre una carretera
horizontal (o trayectoria horizontal).
A B C
0 30 60 90 120 150 X (km)
X (km)
Las gráficas de posición 150
en función del tiempo,
120
NO SON LAS
90
TRAYECTORIAS de los
cuerpos, las gráficas son 60
las HISTORIAS DEL 30
MOVIMIENTO.
18
0 1 2 3 4 5 t (h)

19. ANÁLISIS DEL MRU
En una gráfica de x = f (t) si la pendiente de la recta es:
Positiva, el cuerpo se mueve hacia la derecha.
Negativa, el cuerpo se mueve hacia la izquierda.
Cero, el cuerpo no se mueve o permanece en reposo.
De t = 0 h hasta t = 2 h De t = 2 h hasta t = 3 h
(60 − 0) km (60 − 60) km
v1 = = 30 km / h v2 = = 0 km / h
(2 − 0) h (3 − 2) h
De t = 3 h hasta t = 6 h De t = 6 h hasta t = 8 h
(150 − 60) km (60 − 150) km
v3 = = 30 km / h v4 = = −45 km / h
(6 − 3) h (8 − 6) h
19

20. ANÁLISIS DEL MRU
V (km/h)
30
A1 A3
A2 7 8
0 1 2 3 4 5 6 t (h)
A4
– 45
En una gráfica de v = f (t)
Distancia = suma geométrica de las áreas:
X = A1 + A2 + A3 + A4
X = 60 km + 0 km + 90 km + 90 km = 240 km
Desplazamiento = suma algebraica de las áreas:
ΔX = A1 + A2 + A3 – A4
ΔX = 60 km + 0 km + 90 km – 90 km = 60 km 20

21. Movimiento Rectilíneo Uniforme MRU
PASOS PARA RESOLVER EJERCICIOS DE CINEMÁTICA
1. Establecer el sistema de referencia:
0 20 40 60 80 100 X (km)
2. Dibujar un esquema con la situación propuesta.
3. Establecer el signo de aceleración, velocidad y posición.
V
0 20 40 60 80 100 X (km)
ΔX
21

22. Movimiento Rectilíneo Uniforme MRU
PASOS PARA RESOLVER EJERCICIOS DE CINEMÁTICA
4. Identificar las magnitudes conocidas y desconocidas:
DATOS:
V=____
ΔX=____
Δt=____
5. Asegurarse que todas las unidades son homogéneas.
6. Identificar las ecuaciones del movimiento que servirán
para obtener los resultados.
7. Sustituya los valores en las ecuaciones y realice los
cálculos necesarios. 22

23. Movimiento Rectilíneo Uniforme MRU
PASOS PARA RESOLVER EJERCICIOS DE CINEMÁTICA
8. Compruebe que el resultado sea correcto
matemáticamente y que sea razonable desde el punto
de vista físico.
GRACIAS POR SU
ATENCIÓN
Desde este momento, aplicaremos los conocimientos
adquiridos, para resolver los ejercicios propuestos en
el Módulo de Cinemática
23