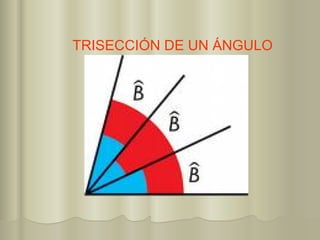
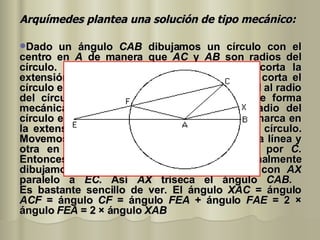
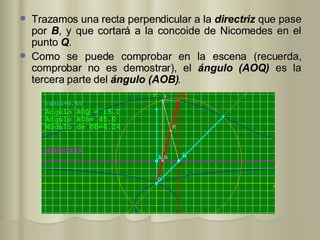
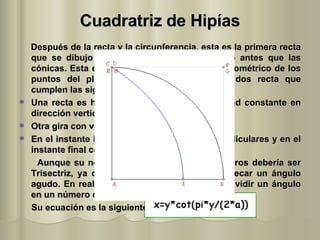
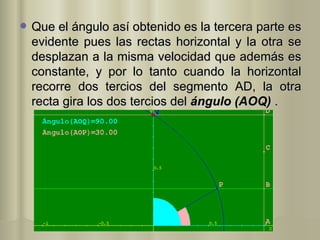
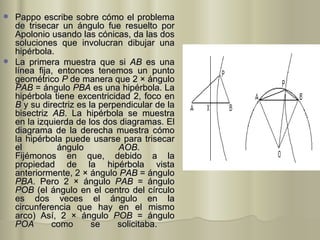
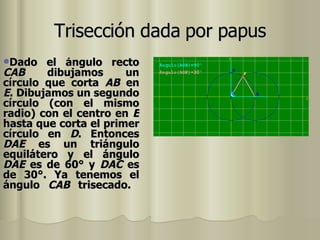
El documento describe varios métodos históricos para trisecar un ángulo, incluyendo los desarrollados por Hipócrates, Arquímedes, Nicomedes, Hipias, MacLaurin, Ceva, Apolonio de Perga y Pappus de Alejandría. Estos métodos involucran el uso de líneas, círculos, hipérbolas, la cuadratriz de Hipias y otras curvas como la concoide de Nicomedes y la cicloide de Ceva.

1. TRISECCIÓN DE UN ÁNGULO

2. INTRODUCCIÓN Hay varias razones por las cuales la trisección del ángulo difiere de los otros problemas clásicos griegos. Primero, no hay una historia real que relate la manera cómo el problema llegó a ser estudiado por primera vez. Segundo, es un problema de otro carácter; no es posible cuadrar un círculo ni duplicar un cubo; sin embargo, sí es posible trisecar ciertos ángulos.

3. HIPÓCRATES Hipócrates , hizo la primera contribución principal a los problemas de ajustar un círculo y de doblar un cubo, también estudió el problema de la trisección de un ángulo. Hay una manera bastante directa al trisectar cualquier ángulo que era conocido por Hipócrates .

4. Funciona de la siguiente manera. Dado un ángulo CAB dibujamos CD perpendicular a AB que corta este segmento en D . Completamos el rectángulo CDAF . Prolongamos FC hasta E y dibujamos la línea AE que corta CD en H . Determinaremos el punto E de manera que se cumpla que HE = 2 AC . De esta forma el ángulo EAB es 1/3 del ángulo CAB . Veamos que G es el punto medio de HE de manera que HG = GE = AC . Ya que ECH es un ángulo recto, CG = HG = GE . Así, el ángulo EAB = ángulo CEA = ángulo ECG . También como AC = CG tenemos el ángulo CAG = ángulo CGA . Pero el ángulo CGA = ángulo GEC + ángulo ECG = 2 × CEG = 2 × EAB como se solicitaba.

5. Arquímedes Arquímedes (287-212 a.C.), notable matemático e inventor griego, que escribió importantes obras sobre geometría plana y del espacio, aritmética y mecánica . Nació en Siracusa, Sicilia, y se educó en Alejandría, Egipto.

6. Arquímedes plantea una solución de tipo mecánico: Dado un ángulo CAB dibujamos un círculo con el centro en A de manera que AC y AB son radios del círculo. Desde C dibujamos una línea que corta la extensión de AB en E . Vemos que esta línea corta el círculo en F y tiene la propiedad que EF es igual al radio del círculo. De nuevo esto puede hacerse de forma mecánica marcando una longitud igual al radio del círculo en la regla y moviéndola teniendo una marca en la extensión de BA y la segunda marca en el círculo. Movemos la regla manteniendo una marca en la línea y otra en el círculo hasta que la línea pase por C . Entonces la línea EC ya está construida. Finalmente dibujamos desde A el radio AX del círculo con AX paralelo a EC . Así AX triseca el ángulo CAB . Es bastante sencillo de ver. El ángulo XAC = ángulo ACF = ángulo CF = ángulo FEA + ángulo FAE = 2 × ángulo FEA = 2 × ángulo XAB

7. Nicomedes Vivió aproximadamente en el tiempo de Arquímedes (en el segundo siglo a.C.) y produjo su famosa curva concoide. De hecho, Nicomedes inventó precisamente esta curva para formalizar el proceso que hemos descrito de rotar una regla manteniendo un punto en una línea. La regla tiene una distancia fija marcada en sí misma y se mantiene una marca en una línea dada mientras los otros puntos definen una curva concoide. Ésta es exactamente la curva necesaria para solucionar el problema de trisecar el ángulo mencionado anteriormente y es así como Nicomedes consiguió resolverlo. El método de Nicomedes fue de un interés más teórico que práctico

8. Trisección de un ángulo agudo usando la Concoide de Nicomedes Trazamos un ángulo agudo, en nuestro caso el ángulo (AOB) . Trazamos una recta perpendicular al lado AO . Esta recta cortará a lado AO en A y al lado OB en B . Construimos la Concoide de Nicomedes con los siguientes elementos: Como Polo el punto O . Como constante la distancia de O a B , es decir k=dist(O,B). Usaremos como directriz , la recta que trazamos perpendicular al lado AO

9. Trazamos una recta perpendicular a la directriz que pase por B , y que cortará a la concoide de Nicomedes en el punto Q . Como se puede comprobar en la escena (recuerda, comprobar no es demostrar), el ángulo (AOQ) es la tercera parte del ángulo (AOB) .

10. Hipías Nació en Elis (Peloponesio) sobre el 430 a.C, fue un estadista y filósofo que viajó de un lugar a otro cobrando por sus servicios. Disertó sobre poesía, gramática, historia, política, matemáticas y astronomía.

11. Cuadratriz de Hipías Después de la recta y la circunferencia, esta es la primera recta que se dibujo (siglo V a.C.), apareció incluso antes que las cónicas. Esta curva se define como el lugar geométrico de los puntos del plano que son intersección de dos recta que cumplen las siguientes condiciones: Una recta es horizontal y se mueve a velocidad constante en dirección vertical. Otra gira con velocidad constante. En el instante inicial ambas rectas son perpendiculares y en el instante final coinciden. Aunque su nombre es Cuadratriz, para nosotros debería ser Trisectriz, ya que la vamos a utilizar para trisecar un ángulo agudo. En realidad con esta curva se puede dividir un ángulo en un número cualquiera de partes iguales. Su ecuación es la siguiente:

12. Trisección de un ángulo agudo con la Cuadratriz de Hipías. Construimos el cuadrado de vértices (0,0);(1,0);(1,1) y (0,1). Trazamos el ángulo, colocando su vértice sobre el Origen y lado sobre el eje horizontal, el otro lado cortara a la cuadratriz en el punto Q. Por Q trazamos una recta horizontal que cortará al lado del en el punto D, como se muestra en la escena de abajo. Se divide el segmento AD en tres partes iguales usando el teorema de Tales, consiguiendo los puntos B,C. Trazando una horizontal por B, se obtienen en la Cuadratriz el punto P que nos proporciona la trisección del ángulo.

13. Que el ángulo así obtenido es la tercera parte es evidente pues las rectas horizontal y la otra se desplazan a la misma velocidad que además es constante, y por lo tanto cuando la horizontal recorre dos tercios del segmento AD, la otra recta gira los dos tercios del ángulo (AOQ) .

14. Trisectriz de MacLaurin (año 1742) Es una curva que fue estudiada por Colin MacLaurin (1698 a 1746) en 1742 cuatro años antes de morir, para intentar dar solución al problema de la trisección del ángulo, de ahí su nombre de Trisectriz.

15. Hay que decir que efectivamente consiguió trisecar un ángulo pero no como los antiguos griegos querían, pues la curva que inventó no se puede trazar sólo con regla y compás, y aunque hoy en día con las nuevas tecnologías es realmente fácil dibujarla con mucha precisión, debemos reconocer el mérito de este hombre para dibujarla en sus tiempos.

16. Trisección de un ángulo agudo con la Trisectriz de MacLaurin . Colocamos el vértice del ángulo en el punto (2*a , 0) y un lado sobre el eje OX en sentido positivo. El lado del ángulo cortará a la Trisectriz de MacLaurin en el Punto Q . El ángulo (AOQ) es un tercio del ángulo (ABQ)

17. La cicloide de Ceva (1699) Tommaso Ceva jesuita y filósofo, nació en Milán el 21 de diciembre de de 1648 y murió también en Milán el 23 de Febrero de 1737.Era hermano de Giovanni Ceva que es mas conocido por su teorema (El teorema de Ceva). Tommaso Ceva enseñó matemáticas en Milán en el colegio Brera y a él se debe la construcción de un aparato mecánico par trazar la cicloide de Ceva (su cicloide), con la cual pudo trisecar un ángulo. La ecuación de cicloide de Ceva es la siguiente:

18. Trisección de un ángulo usando la cicloide de Ceva. El punto A define el ángulo AOB. Trazamos por A una paralela al lado OB, es decir paralela al eje OX. Si G se sitúa en la intersección de la recta anterior con el lazo mayor de la cicloide de Ceva , el ángulo BOG es la trisección del ángulo AOB. Para cada ángulo que definas moviendo el punto A sitúa el punto G en el lugar correspondiente para obtener la trisección .

19. Apolonio de Perga Era conocido como 'el gran geómetra'. Nació: alrededor del 262 a. de C. en Perga, Panfilia, Grecia Jónica (ahora Murtina, Antalia,Turquía) Murió: alrededor del 190 a. de C. en Alejandría, Egipto.

20. Pappo escribe sobre cómo el problema de trisecar un ángulo fue resuelto por Apolonio usando las cónicas, da las dos soluciones que involucran dibujar una hipérbola. La primera muestra que si AB es una línea fija, entonces tenemos un punto geométrico P de manera que 2 × ángulo PAB = ángulo PBA es una hipérbola. La hipérbola tiene excentricidad 2, foco en B y su directriz es la perpendicular de la bisectriz AB . La hipérbola se muestra en la izquierda de los dos diagramas. El diagrama de la derecha muestra cómo la hipérbola puede usarse para trisecar el ángulo AOB . Fijémonos en que, debido a la propiedad de la hipérbola vista anteriormente, 2 × ángulo PAB = ángulo PBA . Pero 2 × ángulo PAB = ángulo POB (el ángulo en el centro del círculo es dos veces el ángulo en la circunferencia que hay en el mismo arco) Así, 2 × ángulo POB = ángulo POA como se solicitaba.

21. Pappus de Alejandría Pappus (Papo) de Alejandría nació alrededor del año 290 en Alejandría, Egipto. Fue el último gran geómetra griego que al parecer vivió siempre en Alejandría. Dedicó muchos de sus trabajos a Pandrosion, Megethion y Hermodorus, éste último al parecer fue su hijo. En los escritos de Proclus se menciona a Pappus como el que encabezaba la Escuela de Alejandría.

22. Trisección dada por papus Dado el ángulo recto CAB dibujamos un círculo que corta AB en E . Dibujamos un segundo círculo (con el mismo radio) con el centro en E hasta que corta el primer círculo en D . Entonces DAE es un triángulo equilátero y el ángulo DAE es de 60° y DAC es de 30°. Ya tenemos el ángulo CAB trisecado.