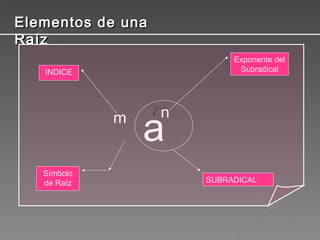
El documento explica los conceptos básicos de las raíces. Define una raíz como una expresión que consta de un índice, un símbolo de raíz y un subradical. Explica que una raíz es equivalente a una potencia con exponente fraccionario y presenta algunas propiedades básicas como la multiplicación y división de raíces de igual índice y la raíz de una raíz. Finalmente, muestra cómo descomponer raíces en términos semejantes.

2. 4 ¿Qué es una Raíz? Una Raíz es una expresión que consta de un INDICE, un símbolo de raíz y un SUBRADICAL. ¿Indice, raíz, cantidad subradical? 2 4 Indice Cantidad Subradical (-5,3) 8 Símbolo de Raíz 2

3. Elementos de una Raíz m a n Exponente del Subradical INDICE SUBRADICAL Símbolo de Raíz

4. _ _ ¿Qué significa la Raíz? (-5,3) 3 = El Índice 2 no se escribe. Una Raíz es una Potencia con Exponente Fracción. 4 2 5 = 5 2 _ 4 2 5 4 3 (-5,3) _ 2 = 3 (-5,3) 6 7 7 6 Raíz Potencia = 3 (-0,6) 2 = (-0,6) 2 3 2 _ = 6 7 7 6

5. Transforma las siguientes Potencia a Raíces Transforma las siguientes raíces a Potencia

6. _ Importante : Lectura de una Raíz. Indice 2, Raíz Cuadrada. Ej. Indice 3, Raíz Cúbica. Ej. Indice 4, Raíz Cuarta. Ej. En General a n b = b n a n b a 0 = 0 b a a 1 = 1 b a ≥ 2 Índice de la raíz y exponente fraccionario

7. Pero es solo una aproximación decimal de la Raíz, que no es exacta. Por lo que la mejor forma de representar a es como . Raíz Cuadrada ya que ya que ya que ya que Esto sucede con muchas raíces cuadradas que no entregan un resultado exacto

8. Pero, al igual que el anterior es solo una aproximación decimal de la Raíz, que no es exacta. Por lo que la mejor forma de representar a es como . Raíz Cúbica ya que ya que ya que ya que Esto sucede con muchas raíces Cúbicas que no entregan un resultado exacto.

9. 2 2 _ El Indice Igual al Exponente. Sabiendo que: 7 2 3 = 3 2 7 3 7 ¿Cuál será el resultado de? 5 2 5 = 5 2 _ 5 5 5 = _ a n = a n a n a a En General: = n 2 1 2 = 2

10. 1 5 _ _ 2 2 _ Multiplicación de Raíces de Igual Indice. Sabiendo que: 7 2 3 = 3 2 7 3 7 ¿Cuál será el resultado de? = 1 2 2 = a n = n x a En General: 5 • 2 • 2 ( _ 2 ) 1 5 • 2 • 5 • m y a a n x • m y

11. Resuelve usando la Propiedad de Potencia: a) b) c) d) e) f) g) h) i) j) Multiplicación de Raíces de Igual Indice.

12. ÷ (7 7 5 _ _ 2 7 _ División de Raíces de Igual Indice. Sabiendo que: 7 2 3 = 3 2 7 3 7 ¿Cuál será el resultado de? = 1 2 = a n = n x En General: 5 ÷ 1 2 _ 2 ) 1 5 7 5 m y a a n x m y ÷ ÷ ÷ ÷

13. Resuelve usando la Propiedad de Potencia: a) b) d) División de Raíces de Igual Indice. c) e) f) h) g)

14. 2 1 • • ( Raíz de una Raíz. ( 7 7 _ _ 7 Sabiendo que: ¿Cuál será el resultado de? 5 5 2 = a = En General: = 1 2 _ 2 1 = 7 m n b •a m n ) _ 2 5 _ 4 5 7 5 4 ( 7 7 _ _ 7 5 5 3 = = 1 2 _ = 7 ) _ 3 5 _ 6 5 7 5 6 3 b 3 2 ) 3 = 3 6 y 2 _ 7 2 3 = 3 2 7 3 7

15. Resuelve usando la Propiedad raíz de raíz: a) b) c) e) d) f) Raíz de una Raíz.

16. Descomponer una Raíz Sabiendo que: Resolver lo siguiente Son términos semejantes

17. Otro ejemplo Son términos semejantes Descomponer una Raíz