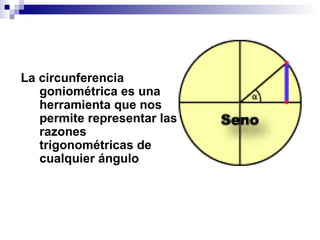
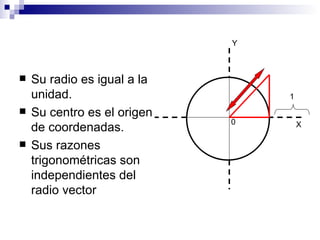
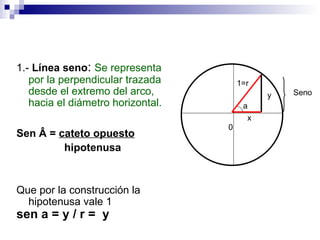
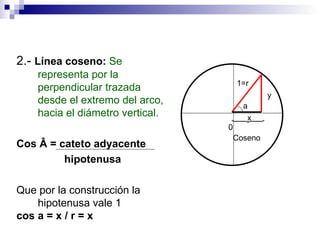
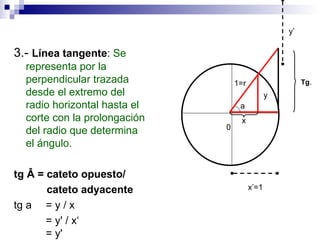
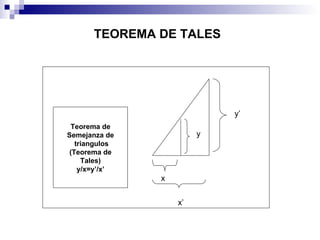
La circunferencia goniométrica representa las razones trigonométricas de cualquier ángulo mediante la construcción de senos, cosenos y tangentes. El seno es la relación entre el cateto opuesto y la hipotenusa, el coseno es la relación entre el cateto adyacente y la hipotenusa, y la tangente es la relación entre el cateto opuesto y el cateto adyacente.

1. TRIGONOMETRIA

2. La circunferencia goniométrica es una herramienta que nos permite representar las razones trigonométricas de cualquier ángulo

3. Su radio es igual a la unidad. Su centro es el origen de coordenadas. Sus razones trigonométricas son independientes del radio vector 0 Y X 1

4. 1.- Línea seno : Se representa por la perpendicular trazada desde el extremo del arco, hacia el diámetro horizontal. Sen  = cateto opuesto hipotenusa Que por la construcción la hipotenusa vale 1 sen a = y / r = y Seno 0 1=r x y a

5. 2.- Línea coseno: Se representa por la perpendicular trazada desde el extremo del arco, hacia el diámetro vertical. Cos  = cateto adyacente hipotenusa Que por la construcción la hipotenusa vale 1 cos a = x / r = x Coseno 0 1=r x y a

6. 3.- Línea tangente : Se representa por la perpendicular trazada desde el extremo del radio horizontal hasta el corte con la prolongación del radio que determina el ángulo. tg  = cateto opuesto/ cateto adyacente tg a = y / x = y' / x‘ = y' Tg . x’=1 0 1=r x y a y’

7. TEOREMA DE TALES x x’ y y’ Teorema de Semejanza de triangulos (Teorema de Tales) y/x=y’/x’