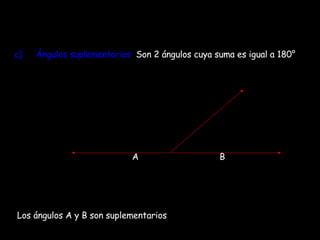
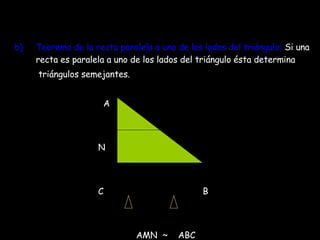
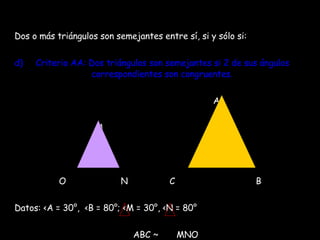
El documento resume conceptos clave de geometría como el teorema de Pitágoras, tipos de ángulos, teoremas sobre ángulos y triángulos, semejanza de triángulos y el teorema de Tales. Explica cómo calcular la hipotenusa o catetos de un triángulo rectángulo usando el teorema de Pitágoras y provee ejemplos. También define ángulos complementarios, suplementarios, opuestos por el vértice y adyacentes, y enuncia teoremas sobre la suma de ángulos

1. MATEMATICAS III CUARTO BIMESTRE

2. TEMA: TEOREMA DE PITÁGORAS Y SEMEJANZA

3. El teorema de Pitágoras es un teorema que se aplica en los triángulos rectángulos y se utiliza para encontrar el valor de la hipotenusa o de alguno de los catetos. En un triángulo rectángulo al lado opuesto al ángulo recto se le llama hipotenusa y a los otros dos lados se les llama catetos. La hipotenusa es siempre mayor a cualquiera de los catetos.

4. El teorema de Pitágoras dice: “ El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos” Su fórmula es: c 2 = a 2 + b 2

5. De la fórmula que describe el teorema de Pitágoras se desprenden las siguientes fórmulas. Fórmula para obtener el valor de la hipotenusa: ______ c = √a 2 + b 2 Fórmula para obtener uno de los catetos: ______ a = √c 2 - b 2

6. Ejemplo 1: Encuentra el valor de la hipotenusa en el siguiente triángulo. a = 3 b = 4 ______ c = √a 2 + b 2 _____ c = √9 + 16 ___ c = √25 c = 5

7. Ejemplo 2: Encuentra el valor de la hipotenusa en el siguiente triángulo. a = 6 b = 8 ______ c = √a 2 + b 2 _____ c = √36 + 64 ___ c = √100 c = 10

8. Ejemplo 1: Encuentra el valor de la incógnita en el siguiente triángulo. c =15 b = 12 ______ a = √c 2 - b 2 ________ a = √225 - 144 ___ a = √81 a = 9

9. EJERCICIOS

10. Una escalera está recargada sobre una casa a un distancia de 1.5 metros. Si la casa tiene una altura de 2.5 metros. ¿Cuánto mide la escalera?

11. Un poste proyecta una sombra de 3metros, y la distancia del punto más alto del poste hasta el punto final de su sombra es de 12 metros. ¿Cuánto mide el poste?

12. Una tabla de 1.6 metros está recargada a una bocina a una distancia de 0.7 metros. ¿Cuál es la altura de a bocina?

13. SUBTEMA: TEOREMAS Y DEFINICIONES

14. Ángulos complementarios: Son 2 ángulos cuya suma es igual a 90 ° A B Los ángulos A y B so complementarios

15. Ángulos suplementarios : Son 2 ángulos cuya suma es igual a 180 ° A B Los ángulos A y B son suplementarios

16. Ángulos opuestos por el vértice: Son los ángulos que en un cruce de dos rectas no comparten lado. A D B C Los ángulos A y C son opuestos por el vértice. Los ángulos B y D son opuestos por el vértice.

17. d) Ángulos adyacentes: Son los ángulos que en un cruce de dos rectas comparten lado. A D B C Los ángulos A y B son adyacentes. Los ángulos A y D son adyacentes.

18. Teorema de la suma de los ángulos interiores de un triángulo: La suma de todos los ángulos interiores de cualquier triángulo es igual a 180 ° A C B < A + < B + < C = 180°

19. Teorema de los ángulos agudos de un triángulo rectángulo: Los ángulos agudos de un triángulo rectángulo son complementarios. A C B < A + < B = 90°

20. Teorema de los ángulos opuestos por el vértice: Los ángulos opuestos por el vértice son congruentes. A = 80 ° D B C Si < A = 80° < C = 80°

21. Teorema de la recta paralela a uno de los lados del triángulo: Si una recta es paralela a uno de los lados del triángulo ésta determina triángulos semejantes. A N M C B AMN ~ ABC

22. SUBTEMA: SEMEJANZA DE TRIÁNGULOS

23. Dos o más triángulos son semejantes entre sí, si y sólo si: Criterio AA: Dos triángulos son semejantes si 2 de sus ángulos correspondientes son congruentes. A M O N C B Datos: <A = 30°, <B = 80°; <M = 30°, <N = 80° ABC ~ MNO

24. Caso LLL: Dos triángulos son semejantes, si tiene sus lados correspondientes proporcionales. A M O N C B Datos: AB = 5cm, BC = 4cm, AC= 3cm; MN = 2.5cm, NO = 2cm, OM = 1.5 cm ABC ~ MNO

25. c) Caso LAL: Dos triángulos son semejantes, si tiene un ángulo congruente entre lados proporcionales. A M O N C B Datos: AB = 6cm, BC = 4cm, <B = 50 °; MN = 35cm, NO = 2cm, N = 50 °; ABC ~ MNO

26. SUBTEMA: TEOREMA DE TALES DE MILETO

27. Teorema de Tales: Teorema que habla de la relación entre segmentos formados cuando rectas transversales cortan a varias rectas paralelas. Este teorema se aplica en triángulos. A A´ B B´ C C´ El teorema de Tales dice: “Si varias paralelas son cortadas por dos Secantes, los segmentos que determinan en una de las secantes son Proporcionales a los segmentos que determinan en la otra secante”