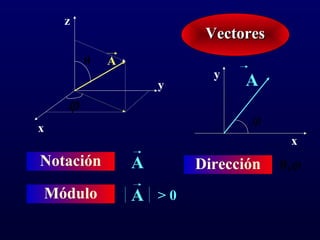
Este documento presenta los conceptos básicos sobre vectores. Define la notación de vectores y sus propiedades como magnitud, dirección y oposición. Explica cómo calcular la suma y resta de vectores, así como la multiplicación por un escalar. También cubre conceptos geométricos como el producto escalar y vectorial entre vectores.

1. z
Vectores
θ A
y
y A
ϕ
ϕ
x
x
Notación A Dirección θ, ϕ
Módulo A >0

2. Propiedades 
de Vectores
A 
B

C
• Dados A y B, si A = B entonces A = B
• Todo vector se puede desplazar paralelamente a
si mismo   
A=B=C

3. Suma de
Vectores A C
B
C
A
B Ley del polígono
R

4. El vector resultante es
aquel que vector que va
desde el origen del primer
vector hasta el extremo del
ultimo

5. Entonces si se tiene los
siguientes vectores
 
A B 
C
 El vector resultante
D
de la suma de todos
ellos será:

6. 
 B 
A C

R 
D
    
R = A+ B +C + D

7. Propiedades  →
de Vectores
A A= A µ

u
-A
Opuesto
Nulo 0 = A + ( -A )

A
Vector unitario μ= 
A

8. Ley
Propiedades
de la suma de Conmutativa
Vectores
R =A+B =B+A
Diferencia Ley Asociativa
         
R = A-B R = A + (B + C) = ( A + B) + C
  
R = A + (-B) -B
R
A
A

9. Ley conmutativa
(Método paralelogramo) A
B +A
+B =
=
A B R
A +B B
B R =
R
Los vectores A y B pueden ser
desplazados paralelamente para
encontrar el vector suma
¿Como se explica esta regla?

10. Multiplicación de un vector por un
escalar
 
Dado dos vectores AyB
 
Se dicen que son paralelos si A = αB
 
si α > 0 A ↑↑ B
 
si α < 0 A ↑↓ B
 
si α = 1 A = B

11. 
A  1 
B= A
 2
B
  1 
A B=− A
 4
B

12. Ejemplo 8:
Hallar el vector resultante de la suma de los
siguientes vectores
A B
C
A B
R = 2C

13. Vectores unitarios en el plano
y
ˆ
j ˆ
i x
ˆ
i Vector unitario en la dirección del eje x +
ˆ
j Vector unitario en la dirección del eje y +

14. Vectores unitarios en el espacio
z
ˆ
k
ˆ
i ˆ
j y
x

19. z
Representación
de un vector Az
θ A
Ay y
Ax ϕ
x
Ax = A cos ϕ sen θ    
A = Ax i + Ay j + Az k
Ay = Asenϕ sen θ 
A = A = Ax2 + Ay + Az2
2
Az = A cos θ

20. Observaciones:
Las componentes rectangulares de
un vector dependen del sistema
coordenado elegido.
La magnitud del vector no cambia.
Permanece invariante en cualquier
sistema coordenado

21. Determínese la resultante de los
siguientes vectores
4u
 + 
3u
A B
  
R = A+ B
7u

22.  
A B
8u
+ 4u = 4u
  
R = A+ B

23. Observamos que, cuando los vectores
están en la misma dirección podemos
determinar fácilmente su magnitud
¿Que sucede si los vectores no están en
la misma dirección ? , ¿ podremos
determinar directamente su magnitud ?

24.  
A B
3u
4u
  
R = A+ B
La magnitud en este caso no puede determinarse
directamente , por lo que debemos tratar de
buscar otra forma de determinarla

25. 
A 
5u
 
3u
Ay B
 By
10
Ax
u
8u
4u

Bx
6u

26.  
A  By
3u
4u
Ay
 
8u
Ax
    B
A = Ax + Ay Bx
  6u 
B = Bx + B y

27. 10u
 
Ax + Bx  
5u
Ay + B y
    
R = Ax + Bx + Ay + B y
Por Pitágoras podemos ahora determinar la magnitud del vector resultante
R = 10 + 5 = 5 5u 2 2

28. 
Ay 
By
 
Ax Bx

Cy 
 Dy
Cx

Dx

29. 
Rx
15 u
5u 
Ry
    
   Rx = Ax + Bx + Cx + Dx
R = Rx + Ry     
R = 5 10 Ry = Ay + By + C y + Dy

30. (x2,y2,z2)

A
(x1,y1,z1)
z
Dados los puntos
indicados el vector que
y los une esta
x
representado por

31. (x2,y2,z2)

A
(x1,y1,z1)
z
y
x 
A = (x 2 − x1 )ˆ + (y 2 − y1 )ˆ + (z2 − z1 )k
i j ˆ

32. Producto  
escalar de dos A ⋅ B = AB cos θ
vectores
Proyección de A sobre B
A B = A cosθ
Proyección de B sobre A
B A = B cosθ

33. Ejemplo 1:
Determinese la suma de los siguientes vectores:

A = 3 ˆ + 8ˆ + 5k
i j ˆ

B = -5 ˆ + 2ˆ − 3k
i j ˆ

C = 4 ˆ − 7ˆ − 2k
i j ˆ

34. Ejemplo 9
Dados los vectores:

A = 3ˆ + 3ˆ − 5k
i j ˆ

B = 4ˆ + 5ˆ − 3k
i j ˆ
Determine :
a) El producto escalar entre ellos.
b) el ángulo que forman entre sí.

35. Área del paralelogramo
Geométricamente, el módulo del producto vectorial de dos vectores
coincide con el área del paralelogramo que tiene por lados a esos vectores.
A=b·h
.

36. Ejemplo
Dados los vectores
Hallar el área del paralelogramo que tiene por lados los vectores
4-(-3)i-(12-(-2))j+(9-2)k

37. Área del triángulo
El área de un triángulo es igual a base por altura partido por 2.
La altura es la recta perpendicular trazada desde un vértice al lado opuesto (o su prolongación).
Ejemplo
Hallar el área del siguiente triángulo:
Área de un triángulo equilátero
Ejemplo
Calcular el área de un triángulo equilátero de 10 cm
de lado.

38. Área de un triángulo rectángulo
El área de un triángulo rectángulo es igual al producto de los catetos partido
por 2.
Ejemplo
Calcular el área del triángulo rectángulo cuyos catetos miden 3
y 4 cm.
Semiperímetro
El semiperímetro de un triángulo es igual a la suma de sus lados partido
por 2.
Se nombra con la letra p.

39. Fórmula de Herón
La fórmula de Herón se utiliza para hallar el área de un triángulo conociendo sus tres
lados.
Ejemplo
Hallar el área del triángulo cuyos lados miden 3, 4
y 5 cm.
Circunferencia circunscrita a un
triángulo
R = radio de la circunferencia
circunscrita

40. Circunferencia inscrita en un triángulo
Conociendo dos lados y el ángulo que forman
r = radio de la circunferencia inscrita
p = semiperímetro

41. Área de un triángulo por
determinantes
Para resolver el determinante de orden tres utilizamos la REGLA DE SARRUS
El determinante está en valor absoluto
Ejemplo
Calcular el área de un triángulo cuyos vértices son: A(2, 0), B(3,4) y C(-2,5).
A(a1,a2), B(b1,b2), C(c1, c2 )
21/2 u2
+ + + - - -
=(8+0+15) -(-8+10+0)= 23-2=21

42. Área de un triángulo por
vectores
Ejemplo
Determinar el área del triángulo cuyos vértices son los puntos A(1, 1, 3), B(2, −1, 5) y C(−3, 3, 1).

48. EJERCICIO PROPUESTOS

49. GRACIAS