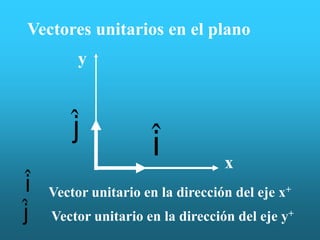
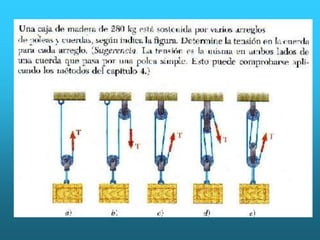
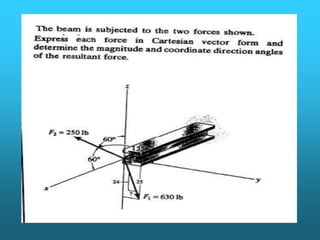
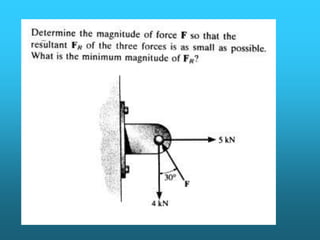
Este documento presenta información sobre vectores unitarios en el plano y en el espacio tridimensional. Define vectores unitarios como vectores cuya magnitud es igual a la unidad y utiliza los símbolos i y j para representar vectores unitarios en las direcciones de los ejes x e y positivos, respectivamente. También cubre conceptos como el producto escalar y vectorial de vectores, sumas y restas vectoriales, y multiplicación de un vector por un escalar.

1. Vectores unitarios en el plano
y
ˆ
j ˆ
i x
ˆ
i Vector unitario en la dirección del eje x+
ˆ
j Vector unitario en la dirección del eje y+

2. Vectores unitarios en el espacio
z
ˆ
k
ˆ
i ˆ
j y
x

3. Producto  
escalar de dos A B AB cos θ
vectores
Proyección de A sobre B
AB A cosθ
Proyección de B sobre A
BA B cosθ

4. Multiplicación de un vector por un
escalar
 
Dado dos vectores AyB
 
Se dicen que son paralelos si A B
 
si 0 A B
 
si 0 A B
 
si 1 A B

5. 
A  1 
B A
 2
B

A
 1
B A
 4
B

6. VECTOR UNITARIO. Es el vector cuya magnitud es igual a la unidad (1)
A
El vector unitario ( u ) de un vec tor ( A ) es igual a u
A
Se usan los símbolos i y j para representa vec toresunitarios,
r
que están en la misma direcc ión de los ejes positivos de los ejes X y
Y
respectivamente. Y A
j Ay j
i X
Ax i X
El vector A se puede escribir como A Ax i Ay j
Para hallar la resultante de 2 ó más vectores, podemos trabajar
sumando las componentes del eje X y Y,
de esos vectores, luego hallamos la resultante con estas dos nuevas
componentes, procedemos de la siguiente manera:
Sean A Ax i Ay j , B Bx i B y j ; el vector resultante
R A B es :
R Ax i Ay j Bx i By j R ( Ax Bx ) i ( Ay By ) j

7. iˆ iˆ 1 iˆ ˆ 0
j
ˆ
j ˆ 1
j iˆ ˆ
k 0
ˆ
k ˆ
k 1 j ˆ
ˆ k 0

A ˆ= A
i
 x
 
A ˆ Ay
j A B A XB X A YB Y A ZB Z

A ˆ
k Az

8. Producto   
vectorial de dos
vectores C A B
C AB sen θ
 
ˆ ˆ 0
i i ˆ ˆ 0
j j

ˆ ˆ
k k 0
j ˆ
iˆ ˆ k j ˆ
ˆ k iˆ
ˆ
k iˆ ˆ
j

9. En tres dimensiones

27. Repaso: Suma

29. Repaso: Resta
(a) (b)

30. y Repaso: Descomposición
vectorial
Fy =Fy j
j
i Fx =Fx i

31. y
Fy
Fx
Fz
Copyright © 1996 by The McGraw-Hill Companies, Inc. All rights reserved.

32. y

33. y
Fy
Fz Fx

34. y
Fy j
cos yj
Fx i
cos zk
cos xi
Fz k

35. Unidades de Prefijo en Ingeniería
Prefijo Abreviación Valor
Tera T 1012
Giga G 109
Mega M 106
Kilo k 103
(nada) 100
Mili m 10-3
Micro 10-6
Nano n 10-9
Pico p 10-12
Fempto f 10-15
Atto a 10-18
35

36. 4. ¿Cuántos mA hay en 2.5 A? 5. ¿Cuántos A hay en 25 mA?
a) 25 mA. a) 25000 A.
b) 250 mA. b) 0.0025 A.
c) 2500 mA. c) 0.025 A.
6. ¿Cuántos mV hay en 2.5 KV? 7. ¿Cuántos KV hay en 25 MV?
a) 25000 KV. a) 25000 MV.
b) 0.025 KV. b) 0.025 MV.
c) 2500000 KV. c) 25000 MV.
36

37. -6 3
1 lit/min = 16,67 * 10 m /s.
3
1 m /s = 60000 lit/min.
1 gal/min = 3,785 lit/min.
-5 3
1 gal/min = 6,309 * 10 m /s.
3
1 pie /s = 449 gal/min.
1 HP= 550 lb-pie/s
1 HP= 746 Watt
1 HP= 0,746 kW

38. Cantidades físicas
Una cantidad física es una propiedad cuantificable o asignable
adscrita a un fenómeno, cuerpo o sustancia particular.
Carga eléctrica
Longitud Tiempo

39. Unidades de medición
Una unidad es una cantidad física particular con la que se comparan otras
cantidades del mismo tipo para expresar su valor.
Un metro es una unidad
establecida para medir longitud.
Con base en la definición, se dice que el
Medición del diámetro es 0.12 m o 12 centímetros.
diámetro del
disco.

40. Unidad SI de medición
para longitud
Un metro es la longitud de la ruta recorrida por una onda luminosa en el
vacío en un intervalo de tiempo de 1/299,792,458 segundos.
1m
1
t segundo
299,792,458

41. Unidad SI de medición de masa
El kilogramo es la unidad de masa – es igual a la masa del prototipo
internacional del kilogramo.
Este estándar es el único
que requiere comparación
para validar un artefacto. En
la Oficina Internacional de
Pesos y Medidas hay una
copia del estándar.

42. Unidad SI de medición de tiempo
El segundo es la duración de 9 192 631 770 periodos de la radiación
correspondiente a la transición entre los dos niveles hiperfinos del estado
base del átomo de cesio 133.
Reloj atómico de fuente de cesio:
El tiempo primario y la frecuencia
estándar para el USA (NIST)

43. Siete unidades fundamentales
Website: http://physics.nist.gov/cuu/index.html
Cantidad Unidad Símbolo
Longitud Metro m
Masa Kilogramo kg
Tiempo Segundo s
Corriente eléctrica Ampere a
Temperatura Kelvin K
Intensidad luminosa Candela cd
Cantidad de Mol mol
sustancia

44. Sistemas de unidades
Sistema SI: Sistema internacional de unidades
establecido por el Comité Internacional de
Pesos y Medidas. Dichas unidades se basan
en definiciones estrictas y son las únicas
unidades oficiales para cantidades físicas.
Unidades usuales en EUA (USCU): Unidades más antiguas todavía de uso
común en Estados Unidos, pero las definiciones se deben basar en
unidades SI.

45. Unidades para mecánica
En mecánica sólo se usan tres cantidades fundamentales: masa, longitud y tiempo.
Una cantidad adicional, fuerza, se deriva de estas tres.
Cantidad Unidad SI Unidad USCS
Masa kilogramo (kg) slug (slug)
Longitud metro (m) pie (ft)
Tiempo segundo (s) segundo (s)
Fuerza newton (N) libra (lb)

46. Procedimiento para convertir unidades
1. Escriba la cantidad a convertir.
2. Defina cada unidad en términos de la
unidad deseada.
3. Por cada definición, forme dos factores de
conversión, uno como recíproco del otro.
4. Multiplique la cantidad a convertir por
aquellos factores que cancelarán todo
menos las unidades deseadas.

47. Ejemplo 1: Convertir 12 in. a centímetros
dado que 1 in. = 2.54 cm.
Paso 1: Escriba la 12 in.
cantidad a convertir.
Paso 2. Defina cada 1 in. = 2.54 cm
unidad en términos
de la unidad deseada. 1 in.
Paso 3. Para cada 2.54 cm
definición, forme dos 2.54 cm
factores de conversión, 1 in
uno como el recíproco
del otro.

48. Ejemplo 1 (cont.): Convertir 12 in. a
centímetros dado que 1 in. = 2.54 cm.
1 in. 2.54 cm
Del paso 3. o
2.54 cm 1 in
Paso 4. Multiplique por aquellos factores que
cancelarán todo menos las unidades deseadas.
Trate algebraicamente los símbolos de unidades.
1 in. in.2 ¡Mala
12 in. 4.72 elección!
2.54 cm cm
¡Respuesta correcta!
2.54 cm
12 in. 30.5 cm
1 in.