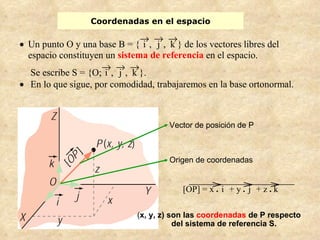
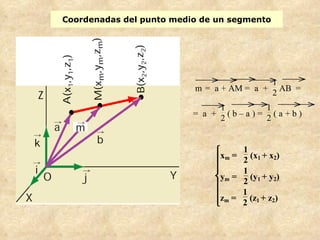
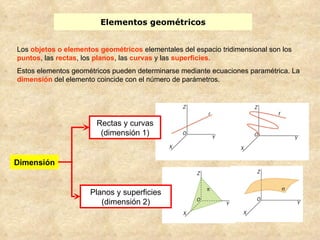
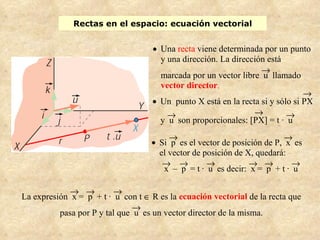
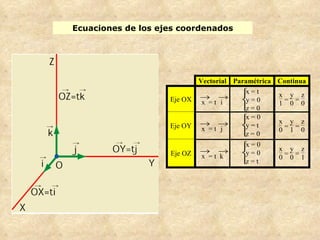
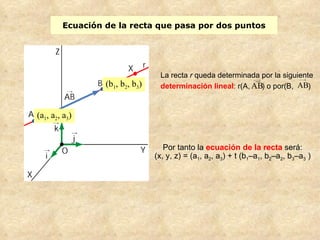
El documento presenta conceptos básicos de geometría en el espacio tridimensional como puntos, rectas, planos y sus ecuaciones vectoriales, paramétricas e implícitas. Explica cómo determinar las ecuaciones de una recta que pasa por dos puntos o es paralela a un vector, así como la ecuación de un plano dado un punto y vector normal o tres puntos.

1. UNIVERSIDAD TECNOLÓGICA CÁLCULO III

3. Coordenadas en el espacio ( x, y, z) son las coordenadas de P respecto del sistema de referencia S. Vector de posición de P Origen de coordenadas

4. Ejes coordenados. Planos coordenados Los tres vectores de la base B determinan con el origen O tres ejes de coordenadas OX, OY, y OZ. Los planos OXY, OYZ y OZX se denominan planos coordenados del sistema de referencia.

5. Coordenadas de un vector libre cualquiera

6. Coordenadas del punto medio de un segmento

7. Elementos geométricos Los objetos o elementos geométricos elementales del espacio tridimensional son los puntos , las rectas , los planos , las curvas y las superficies. Estos elementos geométricos pueden determinarse mediante ecuaciones paramétrica. La dimensión del elemento coincide con el número de parámetros. Dimensión Rectas y curvas (dimensión 1) Planos y superficies (dimensión 2)

8. Rectas en el espacio: ecuación vectorial

9. Rectas en el espacio: ecuaciones paramétricas

10. Rectas en el espacio: ecuación en forma continua Las ecuaciones paramétricas de la recta r que pasa por el punto P (x 0 ,y 0 ,z 0 ) y tienen por vector director (v 1 ,v 2 ,v 3 ) son: Las ecuaciones simétricas de la recta r que pasa por P(x o , y o , z o ) y que tiene por vector director (v1, v2, v3) son: Despejando t en cada una de ellas e igualando, obtenemos las ecuaciones de la recta que no dependen de ningún parámetro

11. Encuentre las ecuaciones vectoriales, paramétricas y simétricas de la recta r que pasa por los puntos P (2, -1, 6) y Q(3, 1, -2). Encuentre las ecuaciones simétricas de la recta que pasa por el punto (1, -2, 4) y es paralela al vector v=i + j - k

12. Rectas en el espacio: ecuación implícita Como la tercera ecuación es combinación lineal de la otras dos, suprimiendo una ellas, la tercera por ejemplo, y operando obtenemos: Este par de ecuaciones es la ecuación de la recta en forma implícita. En general : De aquí obtenemos tres ecuaciones:

13. Ecuaciones de los ejes coordenados

14. Ecuación de la recta que pasa por dos puntos (a 1 , a 2 , a 3 ) (b 1 , b 2 , b 3 ) Por tanto la ecuación de la recta será: (x, y, z) = (a 1 , a 2 , a 3 ) + t (b 1 –a 1 , b 2 –a 2 , b 3 –a 3 ) La recta r queda determinada por la siguiente determinación lineal : r(A,  ) o por(B, )

15. Planos: ecuación vectorial Un plano queda determinado por un punto y dos vectores linealmente independientes. Se dice que a (A, v, w ) es una determinación lineal del plano alfa.   X está en  si y solo si AX es combinación lineal de v y w. Por tanto existirán dos números reales s y t tales que: AX = s v + t w      Por tanto x – a = s v + t w     Y de aquí se obtiene la ecuación vectorial del plano: x = a + s v + t w, con s  R y t  R     Se observa además que X  rango (AX, v, w) = 2  det (AX, v, w) = 0      

16. Planos: ecuaciones paramétricas

17. Notación: por lo general un plano se denota por  Ecuación cartesiana de un plano El plano que contiene a el punto A( x 1, y 1, z 1 ) y tiene un vector normal n= (a, b, c) , este plano consta de todos los puntos B ( x 2, y 2, z 2 ) para los cuales , puede representarse en forma canónica a( x 2 – x 1 ) + b(y 2 – y 1 ) + c(z 2 – z 1 ) = 0 ax +by +cz + d=0 forma general a( x – x 1 ) + b(y – y 1 ) + c(z – z 1 ) = 0 Si B ( x , y , z )

18. Vector normal a un plano Como A (x 1 ,y 1 ,z 1 )   y B (x 2 ,y 2 ,z 2 )   tenemos que: a x 1 + by 1 + cz 1 + d = 0 a x 2 + by 2 + cz 2 + d = 0 Restando término a término obtenemos: a( x 2 – x 1 ) + b(y 2 – y 1 ) + c(z 2 – z 1 ) = 0 (a, b, c) . (x 2 – x 1 , y 2 – y 1 , z 2 – z 1 ) = 0

19. Ejercicio 1. Encuentre un plano que pase por el punto (2. -5, 1) y que tiene un vector normal n= i-2j+3k a( x – x 1 ) + b(y – y 1 ) + c(z – z 1 ) = 0 2. Hallar la ecuación general del plano que contiene a los puntos (2, 1, 1), (0, 4, 1) y (-2, 1, 4)