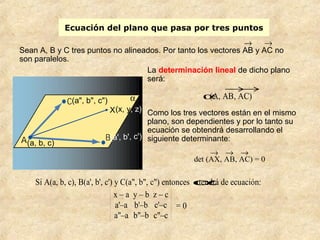
Este documento presenta conceptos básicos sobre coordenadas en el espacio tridimensional. Introduce los sistemas de referencia y coordenadas de puntos. Explica cómo obtener las coordenadas de vectores y segmentos mediante operaciones con vectores. Finalmente, describe elementos geométricos como rectas, planos y sus ecuaciones en diferentes formas, incluyendo paramétricas, vectoriales e implícitas.

1. Presentación elaborada por la profesora Ana Mª Zapatero a
partir de los materiales utilizados en el centro (Editorial SM)
Espacio afín
2º Bachillerato

3. Coordenadas en el espacio
• Un punto O y una base B = {
→
i ,
→
j ,
→
k } de los vectores libres del
espacio constituyen un sistema de referencia en el espacio.
Se escribe S = {O;
→
i ,
→
j ,
→
k }.
• En lo que sigue, por comodidad, trabajaremos en la base ortonormal.
[
→
OP] = x .
→
i + y .
→
j + z .
→
k
(x, y, z) son las coordenadas de P respecto
del sistema de referencia S.
Vector de posición de P
Origen de coordenadas
P’

4. Ejes coordenados. Planos coordenados
• Los tres vectores de la base B
determinan con el origen O
tres ejes de coordenadas
OX, OY, y OZ.
• Los planos OXY, OYZ y OZX
se denominan planos
coordenados del sistema de
referencia.
[
→
OP] = x .
→
i + y .
→
j + z .
→
k

5. Coordenadas de un vector libre cualquiera
•
→
PQ =
→
OQ –
→
OP
• [
→
PQ] =
→
OQ –
→
OP =
= (b – a, b' – a' , b" – a")
• Los puntos P y Q determinan el
vector fijo
→
PQ
•
→
OP +
→
PQ =
→
OQ
Las coordenadas de un vector libre
→
u = [
→
PQ] respecto de la base B =
{
→
i ,
→
j ,
→
k } se obtienen restando las coordenadas del punto P de las
correspondientes de Q en el sistema de referencia S = {O;
→
i ,
→
j ,
→
k }.

6. Coordenadas del punto medio de un segmento





xm =
1
2
(x1 + x2)
ym =
1
2
(y1 + y2)
zm =
1
2
(z1 + z2)
→
m =
→
a +
→
AM =
→
a +
1
2
→
AB =
=
→
a +
1
2
(
→
b –
→
a ) =
1
2
(
→
a +
→
b )

7. Elementos geométricos
Los objetos o elementos geométricos elementales del espacio tridimensional son los
puntos, las rectas, los planos, las curvas y las superficies.
Estos elementos geométricos pueden determinarse mediante ecuaciones paramétricas. La
dimensión del elemento coincide con el número de parámetros.
Dimensión
Rectas y curvas
(dimensión 1)
Planos y superficies
(dimensión 2)

8. Rectas en el espacio: ecuación vectorial
• Una recta viene determinada por un punto
y una dirección. La dirección está
marcada por un vector libre
→
u llamado
vector director.
• Un punto X está en la recta si y sólo si
→
PX
y
→
u son proporcionales: [
→
PX] = t ·
→
u
• Si
→
p es el vector de posición de P,
→
x es
el vector de posición de X, quedará:
→
x –
→
p = t ·
→
u es decir:
→
x =
→
p + t ·
→
u
La expresión
→
x =
→
p + t ·
→
u con t ∈ R es la ecuación vectorial de la recta que
pasa por P y tal que
→
u es un vector director de la misma.
p
x

9. Rectas en el espacio: ecuaciones paramétricas
Las ecuaciones paramétricas de la recta r que pasa por P(xo, yo, zo) y que tiene
por vector director
→
v (v1, v2, v3) son


x = xo + t.v1
y = yo + t.v2
z = zo + t.v3
• La recta que pasa por P de vector director
→
v (v1, v2, v3) se puede poner así:
(x, y, z)= (xo, yo, zo) + t (v1, v2, v3)
Al igualar las coordenadas queda:
(x, y, z) = ( x0+tv1, y0+tv2, z0+tv3)
por lo que

10. Rectas en el espacio: ecuación en forma continua





+=
+=
+=
30
20
10
tvzz
tvyy
tvxx
Las ecuaciones en forma continua de la recta r que pasa por P(xo
, yo
, zo
) y que
tiene por vector director (v1, v2, v3) son:
Despejando t en cada una de ellas e igualando, obtenemos las ecuaciones de
la recta que no dependen de ningún parámetro
Las ecuaciones paramétricas de la recta r que pasa por el punto P (x0,y0,z0) y
tienen por vector director =(v1,v2,v3) son:v


11. Rectas en el espacio: ecuación implícita
Como la tercera ecuación es combinación lineal de la otras dos, suprimiendo
una ellas, la segunda por ejemplo, y operando obtenemos:
Este par de ecuaciones es la ecuación de la recta en forma implícita.
En general :



=+++
=+++
0D'zC'yB'xA'
0DCzByAx
3
0
1
0
v
zz
v
xx −
=
−
2
0
1
0
v
yy
v
xx −
=
−
De aquí obtenemos tres ecuaciones:
2
0
3
0
v
yy
v
zz −
=
−
Las ecuaciones en forma cont ínua de la recta r que pasa por P(x o, yo, zo) y que
tiene por vector director
→
v (v1, v2, v3) son
3
0
2
0
1
0
v
zz
v
yy
v
xx −
=
−
=
−



=−+−
=−+−
0
0
301013
201012
vxvzzvxv
vxvyyvxv

12. Ecuaciones de los ejes coordenados
Vectorial Paramétrica Continua
Eje OX →
x = t
→
i


x = t
y = 0
z = 0
x
1
=
y
0
=
z
0
Eje OY →
x = t
→
j


x = 0
y = t
z = 0
x
0
=
y
1
=
z
0
Eje OZ →
x = t
→
k


x = 0
y = 0
z = t
x
0
=
y
0
=
z
1

13. Ecuación de la recta que pasa por dos puntos
(a1, a2, a3)
(b1, b2, b3)
Por tanto la ecuación de la recta será:
(x, y, z) = (a1, a2, a3) + t (b1–a1, b2–a2, b3–a3 )
La recta r queda determinada por la siguiente
determinación lineal: r(A,  ) o por(B, )AB
→−−
AB
→−−





−+=
−+=
−+=
)(
)(
)(
333
222
111
abtaz
abtay
abtax
33
3
22
2
11
1
ab
az
ab
ay
ab
ax
−
−
=
−
−
=
−
−

14. Planos: ecuación vectorial
Un plano queda determinado por un punto y dos vectores linealmente
independientes. Se dice que a (A, v, w ) es una determinación lineal del plano
α.
→→
Por tanto x – a = s v + t w
→ → → →
Y de aquí se obtiene la ecuación
vectorial del plano:
x = a + s v + t w, con s ∈R y t ∈R
→→ → →
Se observa además que X ∈α ⇔ rango (AX, v, w) = 2 ⇔ det (AX, v, w) = 0
→ →→→→→
X está en α si y solo si AX es
combinación lineal de v y w. Por tanto
existirán dos números reales s y t tales
que:
AX = s v + t w
→ →
→→ →
→

15. Planos: ecuaciones paramétricas y general
Partiendo de la ecuación vectorial del plano:
(x, y, z) = (x1, y1, x1) + t (a, b, c) + s (a', b', c')
obtenemos las ecuaciones paramétricas utilizando las operaciones con
ternas de números de R3
e igualando después. Por tanto las ecuaciones
paramétricas del plano son las siguientes:


x = x1 + ta + sa'
y = y1 + tb + sb'
z = z1 + tc + sc'
x – x1 y– y1 z – z1
a b c
a’ b’ c’
= 0
Como el rango (AX, v, w) = 2 ⇔ det (AX, v, w) = 0 la ecuación general del
plano α se obtiene a partir del determinante
→ →→→→→
y operando queda Ax + By + Cz + D = 0

16. Vector normal a un plano
Observamos que:
→
AB = (x2 – x1, y2 – y1, z2 – z1)
Como A (x1,y1,z1)∈ π y B (x2,y2,z2)∈ π
tenemos que:
ax1 + by1 + cz1 + d = 0
ax2 + by2 + cz2 + d = 0
Restando término a término obtenemos:
a(x2 – x1) + b(y2 – y1) + c(z2 – z1) = 0
(a, b, c) .
(x2 – x1, y2 – y1, z2 – z1) = 0
→
n . [
→
AB] = 0
El vector
→
n es perpendicular a cualquier vector contenido en el plano, es
decir está en una dirección perpendicular al plano. Recibe el nombre de
vector normal al plano. Sus coordenadas son (a,b,c)

17. Planos: ecuación normal
Un punto X(x, y, z) está en el plano si y
sólo si
→
n es perpendicular a
→
MX. Por tanto:
→
n ·
→
MX = 0 ⇔
→
n · (
→
x –
→
m ) = 0
que es la ecuación normal del plano.
Sea M un punto cualquiera del plano α, y
sea (A, B, C) un vector normal al plano.
Desarrollando la expresión anterior
obtenemos:
(A, B, C) · (x – x1 ,y – y1 , z – z1 ) = 0
A( x – x1 ) + B(y – y1 ) + C(z – z1 ) = 0
o bien
A x + B y + C z + D = 0
donde A, B, y C son las componentes
del vector normal al plano.

18. Planos: ecuaciones de los planos coordenados
Vectorial Paramétrica Implícia
Plano OXY →
x = t
→
i + s
→
j


x = t
y = s
z = 0
z = 0
Plano OXZ →
x = t
→
i + s
→
k


x = t
y = 0
z = s
y = 0
Plano OYZ →
x = t
→
j + s
→
k


x = 0
y = t
z = s
x = 0

19. Ecuación del plano que pasa por tres puntos
La determinación lineal de dicho plano
será:
Como los tres vectores están en el mismo
plano, son dependientes y por lo tanto su
ecuación se obtendrá desarrollando el
siguiente determinante:
Sean A, B y C tres puntos no alineados. Por tanto los vectores AB y AC no
son paralelos.
→ →
Si A(a, b, c), B(a', b', c') y C(a", b", c") entonces αtendrá de ecuación:
x – a y – b z – c
a'–a b'–b c'–c
a"–a b"–b c"–c
= 0
α(A,
→
AB,
→
AC)
det (
→
AX,
→
AB,
→
AC) = 0
(a, b, c)
(a", b", c")
(a', b', c')
X(x, y, z)

20. Sean el plano π: ax + by + cz + d = 0 y la recta r
Estudiar las posiciones relativas de recta y plano equivale a estudiar el número
de soluciones del sistema que forman las tres ecuaciones anteriores. Sean A y B
las matrices asociadas a dicho sistema.
Posiciones relativas: recta y plano
Sistema compatible
determinado
Sistema compatible
indeterminado con 1 g.l.
Sistema incompatible
rango(A) = rango (B) = 3 rango(A) = 2; rango (B) = 2 rango(A) = 2; rango (B) = 3
Recta y plano
secantes
Recta contenida
en el plano
Recta y plano
paralelos
1 2 3



=+++
=+++
0''''''''
0''''
dzcybxa
dzcybxa

21. Los vectores normales son
paralelos y A está en π:
A∈π es decir
Los vectores son ortogonales
y A no está en π: A∉π es
decir
Posiciones de recta y plano dados por sus determinaciones
lineal y normal
1
2
3
0· ≠
→→
nAB
0· =
→→
nAB
0· ≠nu

0· =nu

0· =nu

nu

· Condición Posición
Los vectores no son
ortogonales
La recta y el plano
son secantes
y
A∉π
La recta y el plano
son paralelos
y A∈π
La recta está conte-
nida en el plano

22. Posiciones relativas: dos planos
Sean dos planos π: ax + by + cz + d = 0 y π’: a'x + b'y + c'z + d' = 0.
Estudiar las posiciones relativas de ambos planos equivale a estudiar el número de
soluciones del sistema que forman sus ecuaciones. Sean A y B las matrices
asociadas a dicho sistema.
Sistema compatible
indeterminado con 1 g.l.
Sistema incompatible
Sistema compatible
indeterminado con 2 g.l.
rango(A) = rango(B) = 2 rango(A) = 1; rango(B) = 2 rango(A) = rango(B) = 1
a
a' ≠
b
b'
ó
a
a' ≠
c
c'
ó
b
b' ≠
c
c'
a
a'
=
b
b'
=
c
c' ≠
d
d'
a
a'
=
b
b'
=
c
c'
=
d
d'
1 2 3

23. Los vectores normales son
paralelos y A está en π’: A∈π’ ó
Posiciones de dos planos dados por sus determinaciones
normales
1
2
3 αn

βn

Rango 2 Los vectores normales no
son paralelos
Planos secantes
Rango 1
Los vectores normales son
paralelos y A no está en π’:
A∉π’
Planos paralelos
Rango 1 Planos coincidentes
Condición Posición

24. Posiciones relativas: tres planos (I)
Sean π: ax + by + cz + d = 0 y π': a'x + b'y + c'z + d' = 0 y π": a"x + b"y + c"z + d" = 0.
Estudiar las posiciones relativas de estos planos equivale a estudiar el número de soluciones
del sistema que forman sus ecuaciones. Sean A y B las matrices asociadas a dicho sistema.
Los tres planos tienen
un punto en común
Sistema compatible
determinado
rango(A) = rango(B) = 3
Triedro
1
2
a
2
b
Prisma
Los tres planos no tienen
puntos en común
Sistema incompatible
Todos los menores de orden 2
son no nulos
rango(A) = 2; rango(B) = 3
Dos planos paralelos
y un tercero secante a ellos
Los tres planos no tienen
puntos en común
Sistema incompatible
rango(A) = 2; rango(B) = 3
'''' d
d
c
c
b
b
a
a
≠==

25. Sean p: ax + by + cz + d = 0 y p': a'x + b'y + c'z + d' = 0 y p": a"x + b"y + c"z + d" = 0.
Estudiar las posiciones relativas de ambos planos equivale a estudiar el número de soluciones
del sistema que forman sus ecuaciones. Sean A y B las matrices asociadas a dicho sistema.
Posiciones relativas: tres planos (II)
Los tres planos tienen
infinitos puntos
en común
Sistema comp. Ind.
Todos los menores de
orden dos son nulos
rango(A) = rango(B) = 1
Tres planos coincidentes
3a 4
3
b
Tres planos distintos
Los tres planos tienen
una recta en común
Sistema compatible
indeterminado
con 1 g.l.
rango(A) = rango(B) = 2
Dos planos coincidentes
y un tercero secante a ellos
Los tres planos tienen
una recta en común
Sistema comp. ind.
rango(A) = rango(B) = 2
'''' d
d
c
c
b
b
a
a
===

26. Los tres planos no tienen
puntos en común
Sistema incompatible
Todos los menores de orden 2
de A son nulos
rango(A) = 1; rango(B) = 2
Los tres planos no tienen
puntos en común
Sistema incompatible
Hay dos planos con ecuaciones
de coeficientes proporcionales
rango(A) = 1; rango(B) = 2
Tres planos paralelos
Dos planos coincidentes
y un tercero paralelo a ellos
5
a
Sean p: ax + by + cz + d = 0 y p': a'x + b'y + c'z + d' = 0 y p": a"x + b"y + c"z + d" = 0.
Estudiar las posiciones relativas de ambos planos equivale a estudiar el número de
soluciones del sistema que forman sus ecuaciones. Sean A y B las matrices asociadas a
dicho sistema.
5b
Posiciones relativas: tres planos (III)

27. Posiciones relativas: dos rectas (I)
Sea la recta r Sea la recta s
Estudiar las posiciones relativas de ambas rectas equivale a estudiar el número de soluciones
del sistema que forman las cuatro ecuaciones anteriores. Sean A y B las matrices asociadas a
dicho sistema.
Las rectas tienen todos
sus puntos comunes
Sistema compatible
indeterminado con 1 g.l.
rango(A) = rango(B) = 2
Rectas coincidentes
1 2
Rectas paralelas
Las rectas no tienen
puntos en común
Sistema incompatible
rango(A) = 2; rango(B) = 3



=+++
=+++
0""""""""
0"'"'"'"'
dzcybxa
dzcybxa



=+++
=+++
0''''''''
0''''
dzcybxa
dzcybxa

28. Sea la recta r Sea la recta s
Estudiar las posiciones relativas de ambas rectas equivale a estudiar el número de soluciones
del sistema que forman las cuatro ecuaciones anteriores. Sean A y B las matrices asociadas a
dicho sistema.
rango(A) = 3; rango(B) = 4
43
Rectas que se cruzan
Sistema incompatible
Todos los menores de orden 3 son
no nulos
Las rectas no tienen
puntos en común
Posiciones relativas: dos rectas (II)
Rectas secantes
Las dos rectas tienen
un punto en común
Sistema compatible
determinado
rango(A) = rango(B) = 3



=+++
=+++
0''''''''
0''''
dzcybxa
dzcybxa



=+++
=+++
0""""""""
0"'"'"'"'
dzcybxa
dzcybxa

29. Posiciones de dos rectas dados por sus determinaciones
lineales
2
3
αn

βn

1
4
Posición
Rango 2 Rango 3 Se cruzan
Rango 2 Rango 2 Rectas secantes
Rango 1
Rango 1 Rango 1
Rango 2 Rectas paralelas
Rectas coincidentes

30. Haces de planos
Dado ≡Ax+By+Cz+D=0 todos los planos
paralelos tienen el mismo vector normal
por eso los coeficientes de x, y, z, son
todos proporcionales
1 Haz de planos paralelos 2 Haz de planos secantes
Los haces de planos se pueden expresar
como Ax+By+Cz+λ=0 con λ є R.
Dados π≡Ax+By+Cz+D=0
π ′≡ A′x+B′y+C′z+D ′ =0
cualquier combinación lineal de ellos
Pertenece al haz
Los haces de planos se pueden expresar
como Ax+By+Cz+D+ λ(A′x+B′y+C′z+D ′)=0
Para que el haz quede completo hay que
añadir el 2ºplano :A’x+B’y+C’z+D’ = 0