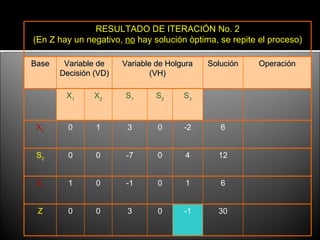
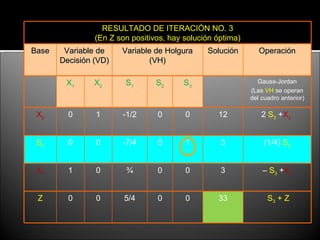
El documento describe el proceso de resolución de un problema de programación lineal mediante el método simplex. Se maximiza la función objetivo Z = 3x1 + 2x2 sujeto a varias restricciones. Tras convertir las desigualdades en igualdades y establecer el tablero inicial, se realizan 3 iteraciones del método simplex que conducen a la solución óptima de x1 = 3, x2 = 12, s3 = 1.

2. Resolver el siguiente problema:
Maximizar Z = 3x1 + 2x2
Sujeto a: 2x1 + x2 ≤ 18
2x1 + 3x2 ≤ 42
3x1 + x2 ≤ 24
x1 ≥ 0 , x2 ≥ 0

3. 1.Convertir las desigualdades en igualdades: Se introduce una variable
de holgura por cada una de las restricciones, en este caso s1, s2, s3 .
2x1 + x2 + s1 = 18
2x1 + 3x2 + s2 = 42
3x1 + x2 + s3 = 24
8.Igualar la función objetivo a cero
Z - 3x1 - 2x2 = 0
12.Escribir el tablero inicial simplex: En las columnas aparecerán todas
:
las variables del problema y, en las filas, los coeficientes de las igualdades
obtenidas, una fila para cada restricción y la última fila con los coeficientes
de la función objetivo.
objetivo

4. 1. -Encontrar la Variable de Decision que entra en la base y la
Variable de Holgura que sale de la base
VD Base (Columnas )
VH Base (Filas)
-Para escoger la Variable de Decision que entra en la base,
observamos la ultima fila, escogemos la variable con el coeficiente
màs negativo = columna pivote.
Nota Si en la última fila no existiese ningún coeficiente negativo, significa que
se ha alcanzado la solución optima
-Para escoger la variable de holgura que sale de la base, se divide
cada término de la última columna (valores solución) por el término
correspondiente de la columna pivote = fila pivote

5. Tablero Inicial
Base Variable de Variable de Holgura Solución
Decisión (VD) (VH)
X1 X2 S1 S2 S3
S1 2 1 1 0 0 18
S2 2 3 0 1 0 42
S3 3 1 0 0 1 24
Z -3 -2 0 0 0 0

6. ITERACIÓN No. 1
(Buscar fila y columna pivote)
Base Variable de Variable de Holgura Solución Operación
Decisión (VD) (VH)
X1 X2 S1 S2 S3 División
prueba
S1 2 1 1 0 0 18 18/2 = 9
S2 2 3 0 1 0 42 42/2 = 21
S3 3 1 0 0 1 24 24/3 = 8
Z -3 -2 0 0 0 0

7. RESULTADO DE ITERACIÓN No. 1
(Por operaciones convertimos elemento pivote =1 y después ceros los otros elementos de la
columna pivote)
Base Variable de Variable de Holgura Solución Operación
Decisión (VD) (VH)
X1 X2 S1 S2 S3 Gauss-Jordan
(Las VH se operan del
cuadro anterior)
S1 0 1/3 1 0 -2/3 2 – 2 (X1) +S1
S2 0 7/3 0 1 -2/3 26 – 2 (X1) + S2
X1 1 1/3 0 0 1/3 8 (1/3) X1
Z 0 -1 0 0 1 24 3 (X1) +Z

8. RESULTADO DE ITERACIÓN NO. 1
(En Z hay un negativo, no hay solución óptima, se repite el proceso)
Base Variable de Variable de Holgura Solución Operación
Decisión (VD) (VH)
X1 X2 S1 S2 S3
S1 0 1/3 1 0 -2/3 2
S2 0 7/3 0 1 -2/3 26
X1 1 1/3 0 0 1/3 8
Z 0 -1 0 0 1 24

9. ITERACIÓN No. 2
(Buscar fila y columna pivote)
Base Variable de Variable de Holgura Solución Operación
Decisión (VD) (VH)
X1 X2 S1 S2 S3 División
Prueba
S1 0 1/3 1 0 -2/3 2 2/(1/3) = 6
S2 0 7/3 0 1 -2/3 26 26/(7/3) = 78/7
X1 1 1/3 0 0 1/3 8 8/(1/3) = 24
Z 0 -1 0 0 1 24

10. RESULTADO DE ITERACIÓN No. 2
(Por operaciones convertimos elemento pivote =1 y después ceros los otros elementos de la columna
pivote)
Base Variable de Variable de Holgura Solución Operación
Decisión (VD) (VH)
Gauss-Jordan
X1 X2 S1 S2 S3
(Las VH se operan del
cuadro anterior)
X2 0 1 3 0 -2 6 3X2
S2 0 0 -7 0 4 12 – (7/3) (X2)+S2
X1 1 0 -1 0 1 6 – (1/3) (X2)+X1
Z 0 0 3 0 -1 30 X2+Z

11. RESULTADO DE ITERACIÓN No. 2
(En Z hay un negativo, no hay solución òptima, se repite el proceso)
Base Variable de Variable de Holgura Solución Operación
Decisión (VD) (VH)
X1 X2 S1 S2 S3
X2 0 1 3 0 -2 6
S2 0 0 -7 0 4 12
X1 1 0 -1 0 1 6
Z 0 0 3 0 -1 30

12. ITERACIÓN No. 3
(Buscar fila y columna pivote)
Base Variable de Variable de Holgura Solución Operación
Decisión (VD) (VH)
X1 X2 S1 S2 S3
X2 0 1 3 0 -2 6 No se toma por
ser negativo
S2 0 0 -7 0 4 12 12/4 = 3
X1 1 0 -1 0 1 6 6/1 = 6
Z 0 0 3 0 -1 30

13. RESULTADO DE ITERACIÓN NO. 3
(En Z son positivos, hay solución óptima)
Base Variable de Variable de Holgura Solución Operación
Decisión (VD) (VH)
X1 X2 S1 S2 S3 Gauss-Jordan
(Las VH se operan
del cuadro anterior)
X2 0 1 -1/2 0 0 12 2 S3 +X2
S3 0 0 -7/4 0 1 3 (1/4) S3
X1 1 0 ¾ 0 0 3 – S3 +X1
Z 0 0 5/4 0 0 33 S3 + Z

14. TABLERO FINAL
Base Variable de Variable de Holgura Solución
Decisión (VD) (VH)
X1 X2 S1 S2 S3
X2 0 1 -1/2 0 0 12
S3 0 0 -7/4 0 1 3
X1 1 0 3/4 0 0 3
Z 0 0 5/4 0 0 33