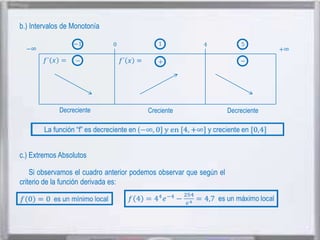
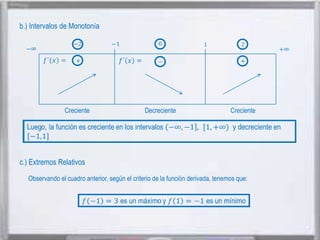
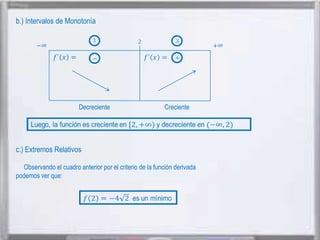
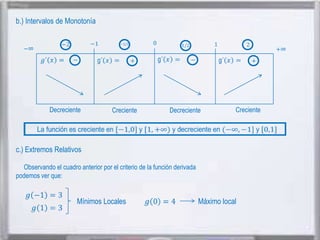
El documento presenta información sobre Gottfried Leibniz, matemático alemán que desarrolló el cálculo infinitesimal independientemente de Isaac Newton. Leibniz nació en Alemania en 1646 y se graduó de la Universidad de Altdorf, donde luego se desempeñó como profesor. En 1684 publicó sus investigaciones sobre el cálculo diferencial e integral. Más tarde, surgió una disputa entre Leibniz y Newton sobre quién había inventado el cálculo.

2. Integrantes:
• Agrela, Kenedy
• Dos Santos, Edgar
• Escorcia, Stephany
• Oropeza, Jiselis
• Suarez, Maria

6. Gottfried Wilhelm nació
en Leipzig, Alemania. Se graduó
y fue profesor de la universidad
de Altdor. Se desenvolvió con
excelencia en varios campos:
Matemática,
Filosofía,
Diplomacia, etc.
En 1684 se publicaron
sus investigaciones de lo que
seria el Calculo Diferencial e
Integral. El, junto con Newton,
son
considerados
como
creadores del calculo. Invento
una maquina de multiplicar.
Siendo embajador de
Paris, conoció a científicos,
como
Huygens,
quienes
reforzaron su interés por la
matemática.
En 1712, surgió una
larga e infortunada discordia
entre Newton y sus seguidores,
por un lado, y Leibniz y sus
seguidores, en otro lado, sobre
quien de los matemáticos
realmente invento el calculo. Se
lanzaron acusaciones mutuas
de plagio y deshonestidad. Los

9. Derivamos término a término

11. (Efectuando las Derivadas)

13. (Efectuando las derivadas)

15. (Efectuando los derivados indicados)
(Agrupando terminos semejantes)

17. (Efectuando los derivados
indicados)
(Agrupando términos semejantes)
(Factor Común)

19. 1
2
3
4
5
6
7
8
9
10

22. Al derivar una función “f” obtenemos la función derivada “f ” podemos
volver a derivarla obteniendo otra nueva función “(f ) ”, cuyo dominio es el conjunto
de todos los puntos “x” del dominio “f ” para los cuales “f ” es derivable en “x”; o sea
todos los puntos “x” del dominio “f ” para los cuales existe el siguiente limite:
En vista de que “f´´” es la segunda derivada de “f ”, a “f´” la llamaremos primera derivada de
“f ”.

24. Hallar la primera y segunda derivada de
cada una de las siguientes funciones:

25. Hallar la primera y segunda derivada de
cada una de las siguientes funciones:

33. 1
2
3
4
5

35. Es una propiedad de las funciones derivables en un intervalo. Algunos matemáticos consideran
que este teorema es el más importante de cálculo. El teorema no se usa para resolver problemas
matemáticos; más bien, se usa normalmente para demostrar otros teoremas. El teorema de valor
medio puede usarse para demostrar el teorema de Taylor ya que es un caso especial.
El teorema del valor medio es un resultado fuerte. Gracias a él podemos obtener información de
la función F a partir de su función derivada F'. Por ejemplo, es fácil demostrar, usando este
teorema, que si F'(x) es positiva en un intervalo, entonces F ha de ser creciente en ese intervalo.
Numero crítico de una función de una variable real es cualquier valor en el dominio en donde la
función no es diferenciable o cuando su derivada es 0.1 2 El valor de la función en el punto crítico
es un valor crítico de la función. Estas definiciones admiten generalizaciones a funciones de
varias variables, mapas diferenciables entre Rm y Rn, y mapas diferenciables entre variedades
diferenciables.
Ejemplo: La función ƒ(x) = x2 + 2x + 3 es diferenciable en todo lugar, con la derivada ƒ′(x) = 2x +
2. Esta función tiene un único punto crítico −1, debido a que es el único número x0 para el cual
2x0 + 2 = 0. Este punto es un mínimo global de ƒ. El correspondiente valor crítico es ƒ(−1) = 2. La
gráfica de ƒ es una parábola cóncava hacia arriba, el punto crítico es la abscisa del vértice,
donde la línea tangente es horizontal, y el valor crítico es la ordenada del vértice y puede ser
representado por la intersección de esta línea tangente y el eje y.

36. Compruebe la hipótesis del teorema del valor medio
para la función
es el.
Hallar el valor de “c” que satisface la conclusión del
teorema del valor medio.
Así,

37. Ahora,
Luego,

38. Hallar todos los números “c” que satisfacen la
conclusión del teorema del valor medio, la función
en

41. Dada la función
, hallar:
a.) Numero critico ; b.) Intervalos de Monotonía (ascendientes
c.) Los Extremos ; y decrecientes).
e.) Puntos de
Inflexión.
d.) Intervalo de Concavidad

42. Dada la función
, hallar:
a.) Numero critico ; b.) Intervalos de Monotonía (ascendientes
c.) Los Extremos ; y decrecientes).
e.) Puntos de
Inflexión.
d.) Intervalo de Concavidad
a.) Números Críticos
(Derivando)
(Igualamos “a” con la derivada
y despejamos “a” ; “x” )
Luego, los numero críticos son
Y

43. b.) Intervalos de Monotonía
Decreciente
Creciente
c.) Extremos Absolutos
Si observamos el cuadro anterior podemos observar que según el
criterio de la función derivada es:
Decreciente

44. d.) Intervalo de la Concavidad

45. Los números críticos de segundo orden son: 0, 6, 2
Decreciente
e.) Puntos de Inflexión
Creciente
Decreciente

46. Dada la función
, hallar:
a.) Numero critico ; b.) Intervalos de Monotonía (ascendientes
c.) Los Extremos ; y decrecientes).
e.) Puntos de
Inflexión.
d.) Intervalo de Concavidad

47. Dada la función
, hallar:
a.) Numero critico ; b.) Intervalos de Monotonía (ascendientes
c.) Los Extremos ; y decrecientes).
e.) Puntos de
Inflexión.
a.) Números Críticos
d.) Intervalo de Concavidad

48. b.) Intervalos de Monotonía
Creciente
Decreciente
c.) Extremos Relativos
Observando el cuadro anterior por el criterio de la función derivada
podemos ver que:

49. d.) Intervalos de Concavidad
e.) Puntos de Inflexión

50. Dada la función
, hallar:
a.) Numero critico ; b.) Intervalos de Monotonía (ascendientes
c.) Los Extremos ; y decrecientes).
e.) Puntos de
Inflexión.
d.) Intervalo de Concavidad

51. Dada la función
, hallar:
a.) Numero critico ; b.) Intervalos de Monotonía (ascendientes
c.) Los Extremos ; y decrecientes).
e.) Puntos de
Inflexión.
a.) Números Críticos
d.) Intervalo de Concavidad

52. b.) Intervalos de Monotonía
Creciente
Decreciente
Creciente
c.) Extremos Relativos
Observando el cuadro anterior, según el criterio de la función derivada, tenemos que:

53. d.) Intervalos de Concavidad
Decreciente
Creciente

54. e.) Puntos de Inflexión

55. Dada la función
, hallar:
a.) Numero critico ; b.) Intervalos de Monotonía (ascendientes
c.) Los Extremos ; y decrecientes).
e.) Puntos de
Inflexión.
d.) Intervalo de Concavidad

56. Dada la función
, hallar:
a.) Numero critico ; b.) Intervalos de Monotonía (ascendientes
c.) Los Extremos ; y decrecientes).
e.) Puntos de
Inflexión.
a.) Números Críticos
d.) Intervalo de Concavidad

57. b.) Intervalos de Monotonía
Decreciente
Creciente
c.) Extremos Relativos
Observando el cuadro anterior por el criterio de la función derivada
podemos ver que:

58. d.) Intervalos de Concavidad

59. Decreciente
e.) Puntos de Inflexión
Creciente

60. Dada la función
, hallar:
a.) Numero critico ; b.) Intervalos de Monotonía (ascendientes
c.) Los Extremos ; y decrecientes).
e.) Puntos de
Inflexión.
d.) Intervalo de Concavidad

61. Dada la función
, hallar:
a.) Numero critico ; b.) Intervalos de Monotonía (ascendientes
c.) Los Extremos ; y decrecientes).
e.) Puntos de
Inflexión.
a.) Números Críticos
d.) Intervalo de Concavidad

62. b.) Intervalos de Monotonía
Decreciente
Creciente
Decreciente
Creciente
c.) Extremos Relativos
Observando el cuadro anterior por el criterio de la función derivada
podemos ver que:
Mínimos Locales
Máximo local

63. d.) Intervalos de Concavidad
Números críticos de segundo orden
y

64. Creciente
e.) Puntos de Inflexión
Decreciente
Creciente

66. Dada las siguientes funciones, hallar:
a.) Numero critico ;
b.) Intervalos de Monotonía (ascendientes y decrecientes).
c.) Los Extremos ;
e.) Puntos de
Inflexión.
d.) Intervalo de Concavidad
1
2
3
4
5