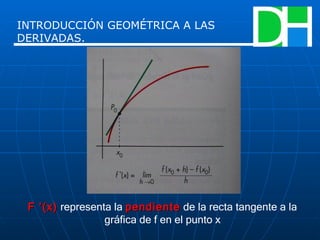
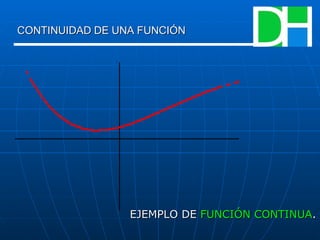
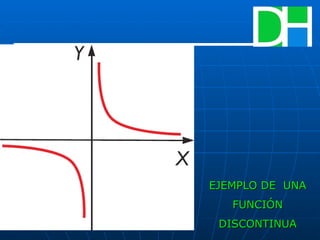
Este documento trata sobre el tema de la derivada. Explica brevemente la historia de la derivada y cómo surgió del estudio de problemas geométricos como la tangente a una curva y los extremos. Define la derivada como el límite que representa la pendiente de la recta tangente a una función en un punto. También cubre conceptos como la derivabilidad, las fórmulas de derivación, y la continuidad y discontinuidad de funciones.

1. LA DERIVADA -Paco Calvo Moreno 1º C

2. ÍNDICE 1.- Historia de la derivada. 2.- Concepto de derivada. 3.- Derivada de una función. 4.- Teoremas de derivadas 5.- Introducción geométrica a las derivadas.

3. 6.- Fórmulas de derivación. 7.- Derivación de operación de funciones 8.- Derivación de composición de funciones. 9.- Continuidad de una función. 10.-Discontinuidad de una función íNDICE

4. HISTORIA DE LA DERIVADA Los problemas típicos que dieron origen al Cálculo infinitesimal , comenzaron a plantearse en la época de la Grecia clásica ( siglo III a.c ), pero no se encontraron métodos sistemáticos de resolución hasta veinte siglos después (en el siglo XVII por obra de Newton y Leibniz ).

5. HISTORIA DE LA DERIVADA Existen dos conceptos de tipo geométrico que dieron origen a las derivadas : El problema de la tangente a una curva El problema de los extremos: máximos y mínimos En su conjunto dieron origen a lo que se conoce como cálculo diferencial .

6.  La derivada es uno de los conceptos más importantes en matemáticas : es el resultado de un límite y representa la pendiente de la recta tangente a la gráfica de la función en un punto .  La definición de derivada es la siguiente:  No se puede olvidar que podría no existir tal límite y ser la función, por tanto, no derivable en ese punto. CONCEPTO DE DERIVADA

7. DERIVADA DE UNA FUNCIÓN  Dada una función para hallar su derivada podemos hacerlo de dos formas : mediante el límite anterior. mediante la tabla de derivadas .

8. DERIVADA DE UN FUNCIÓN

9.  1.- Si una función no es continua en un punto , entonces no es derivable en ese punto . Pero si la función es continua en ese punto puede o no ser derivable.  2.- Si un función es continua en un punto y ese punto es anguloso o de distinta curvatura entonces no es derivable en ese punto. TEOREMAS DE DERIVADAS

10. INTRODUCCIÓN GEOMÉTRICA A LAS DERIVADAS Supongamos que tenemos una función y la llamamos f(x) . La derivada de f(x) es otra función que llamaremos f ’(x). F ’(x) representa la pendiente de la recta tangente a la gráfica de f en el punto x . La pendiente es la inclinación de la línea recta que pasa justo por encima del punto x y que es tangente a la gráfica de f(x)

11. INTRODUCCIÓN GEOMÉTRICA A LAS DERIVADAS. F ’(x) representa la pendiente de la recta tangente a la gráfica de f en el punto x

12. Si aplicamos lo antes expuesto, al identificar dos puntos muy cercanos en la gráfica y unirlos mediante una línea recta, la pendiente queda visualizada . Cuanto más cercanos sean los dos puntos que se unen por medio de la recta, la recta se parece más a una recta tangente a la gráfica y su pendiente se parece más a la pendiente de una recta tangente . INTRODUCCIÓN GEOMÉTRICA A LAS DERIVADAS

13.  hemos de relacionar la pendiente con la rapidez , de manera que la pendiente coincide con la rapidez con que aumenta el valor de la función en cada punto si la pendiente en un punto es muy grande , entonces el valor de la función en ese punto crece muy deprisa ; si es pequeña , entonces el valor de la función crece despacio en ese punto. INTRODUCCIÓN GEOMÉTRICA A LAS DERIVADAS

14.  Según lo anterior, tanto la pendiente de la recta tangente como la rapidez de crecimiento en un punto de una función está dado por f ’(x). Pero, no todas las funciones poseen derivada , situación que geométricamente se explica porque no se puede definir la pendiente a una recta tangente en una función que no es continua . Incluso hay funciones donde cualquier recta que pase por uno de sus puntos interseca en una infinidad de puntos muy cercanos y por tanto no hay recta tangente. INTRODUCCIÓN GEOMÉTRICA A LAS DERIVADAS (II)

15.  Las funciones que poseen derivada se llaman diferenciables . Conocer la derivada de una función diferenciable es generalmente sencillo utilizando las técnicas de derivación desarrolladas por Leibniz y Newton  permiten conocer las derivadas de muchas de las funciones de interés frecuente, o bien, simplificar el trabajo para encontrar derivadas menos comunes. INTRODUCCIÓN GEOMÉTRICA A LAS DERIVADAS (II)

16. FÓRMULAS DE DERIVACIÓN

17. FÓRMULAS DE DERIVACIÓN ( II )

18. FÓRMULAS DE DERIVACIÓN ( III )

19. FÓRMULAS DE DERIVACIÓN ( IV )

20. DERIVACIÓN DE OPERACIÓN DE FUNCIONES

21. DERIVACIÓN DE COMPOSICIÓN DE FUNCIONES

22. Se dice que una función f(x) es continua en un punto x = a , si y sólo si , se cumplen las tres condiciones siguientes :  1. Que el punto x = a tenga imagen  2. Que exista el límite de la función en el punto x = a .  3. Que la imagen del punto coincida con el límite de la función en el punto. CONTINUIDAD DE UNA FUNCIÓN

23. EJEMPLO DE FUNCIÓN CONTINUA . CONTINUIDAD DE UNA FUNCIÓN

24. DISCONTINUIDAD DE UNA FUNCIÓN Una función discontinua es aquella que no puede dibujarse de un solo trazo. Es decir, existen puntos donde de una pequeña variación de la variable independiente produce un salto en los valores de la variable dependiente .  Estos puntos reciben el nombre de puntos de discontinuidad de la función.

25. EJEMPLO DE UNA FUNCIÓN DISCONTINUA