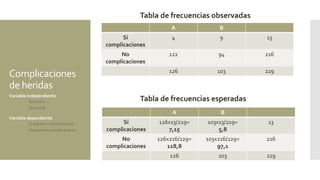
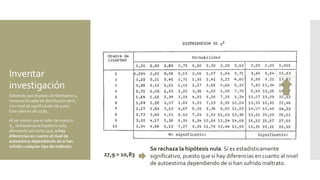
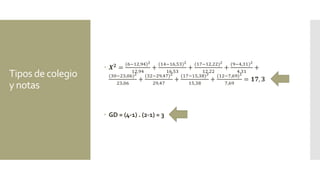
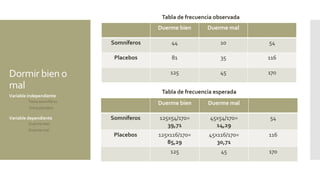
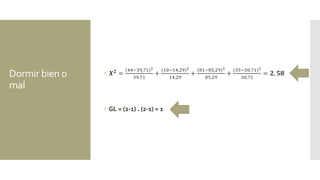
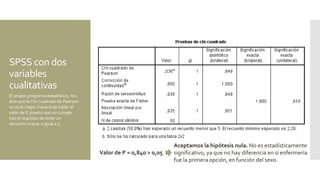
Este documento presenta resúmenes de varios ejercicios y ejemplos de uso de la prueba de chi cuadrado. Incluye ejemplos sobre la relación entre complicaciones quirúrgicas y tipo de servicio hospitalario, nivel de autoestima y experiencia de maltrato, y efecto del tipo de colegio en las calificaciones de religión. Explica cómo calcular chi cuadrado a mano y usarla en SPSS para determinar si hay diferencias estadísticamente significativas entre grupos.

1. Seminario 8
Chi cuadrado de Pearson
Blanca Iglesias

2. Ejercicios

3. Ejercicios
Complicaciones
de heridas
Inventar
investigación
Tipos de
colegio y notas
Dormir bien o
mal
SPSS con dos
variables
cualitativas

4. Complicaciones
de heridas
Se está estudiando la relación de complicaciones en la
herida quirúrgica de dos servicios hospitalarios (A, B).
Para ello, hemos recogido las observaciones de dos
servicios durante un periodo de tiempo.
H0. No hay diferencia entre los servicios (en los dos existe la misma
probabilidad de complicaciones de la herida quirúrgica)
H1. Existe la diferencia entre los servicios.
Queremos trabajar a un nivel de significación de 0,05
(95%)

5. Complicaciones
de heridas
A B
Sí
complicaciones
4 9 13
No
complicaciones
122 94 216
126 103 229
Variable independiente
- ServicioA
- Servicio B
Variable dependiente
- Sí aparecen complicaciones
- No aparecen complicaciones
Tabla de frecuencias observadas
A B
Sí
complicaciones
126x13/229=
7,15
103x13/229=
5,8
13
No
complicaciones
126x216/229=
118,8
103x216/229=
97,1
216
126 103 229
Tabla de frecuencias esperadas

6. Complicaciones
de heridas  𝑮𝒓𝒂𝒅𝒐 𝒅𝒆 𝒍𝒊𝒃𝒆𝒓𝒕𝒂𝒅 = (𝑛º 𝑑𝑒 𝑐𝑎𝑡𝑒𝑔𝑜𝑟í𝑎𝑠 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒 𝑖𝑛𝑑𝑒𝑝𝑒𝑛𝑑𝑖𝑒𝑛𝑡𝑒 −
1) ∙ (𝑛º 𝑑𝑒 𝑐𝑎𝑡𝑒𝑔𝑜𝑟í𝑎𝑠 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒 𝑑𝑒𝑝𝑒𝑛𝑑𝑖𝑒𝑛𝑡𝑒 − 1)Calculamos chi cuadrado a partir de
la fórmula.
A continuación calculamos los
grados de libertad a partir también
de la fórmula.
2
2 ( )fo ft
ft


 
       
2 2 2 22
2 4 7,15 9 5,8 122 118,8 94 97,1( )
3,27
7,15 5,8 118,8 97,15
fo ft
ft

   
     
GL = (2-1) . (2-1) = 1

7. Complicaciones
de heridas
Sabiendo que el grado de libertad es 1,
miramos la tabla de distribución de X2
con nivel de significación del 95%. Este
valor es de 3,84.
Al ser mayor que el valor de nuestra
X2, aceptamos la hipótesis nula,
afirmando por tanto que, no hay
diferencia entre los servicios (en los
dos existe la misma probabilidad de
complicaciones de la herida
quirúrgica).
3,27 < 3,84
Se acepta la hipótesis nula. No es estadísticamente
significativo ya que no hay diferencias entre los servicios, ya
que los dos tienen la misma posibilidad de complicaciones
en las heridas quirúrgicas.

8. Inventar
investigación
Inventa el tema de investigación a un
nivel de significación de 0,001.
X2 = 27,9
20 45
70 26

9. Inventar
investigación
 Se está estudiando la relación del nivel de autoestima de
determinados pacientes, y si han sufrido o no cualquier tipo de
maltrato. Para ello, hemos recogido las observaciones de dos
servicios durante un periodo de tiempo.
 H0. No hay diferencias en el nivel de autoestima de determinados
pacientes dependiendo de si han sufrido o no cualquier tipo de maltrato.
 H1. Sí hay diferencias en el nivel de autoestima de determinados
pacientes dependiendo de si han sufrido o no cualquier tipo de maltrato.
 𝑿 𝟐
=
(20−36,3)2
36,3
+
(45−28,6)2
28,6
+
(70−53,6)2
53,6
+
(26−42,3)2
42,3
= 𝟐𝟕, 𝟗
 GL = (2-1) . (2-1) = 1
2
2 ( )
27,9
fo ft
ft


 

10. Inventar
investigación
Sí maltrato No maltrato
Alta autoestima 20 45 65
Baja autoestima 70 26 96
90 71 161
Variable independiente
- Sí ha sufrido maltrato
- No ha sufrido maltrato
Variable dependiente
- Autoestima alta
- Autoestima baja
Sí maltrato No maltrato
Alta autoestima 90x65/161=
36,3
71x65/161=
28,6
65
Baja autoestima 90x96/161=
53,6
71x96/161=
42,3
96
90 71 161
Tabla de frecuencias observadas
Tabla de frecuencias esperadas

11. Inventar
investigación
Sabiendo que el grado de libertad es 1,
miramos la tabla de distribución de X2
con nivel de significación de 0,001.
Este valor es de 10,83.
Al ser menor que el valor de nuestra
X2, rechazamos la hipótesis nula,
afirmando por tanto que, sí hay
diferencias en cuanto al nivel de
autoestima dependiendo de si han
sufrido cualquier tipo de maltrato.
27,9 > 10,83
Se rechaza la hipótesis nula. Sí es estadísticamente
significativo, puesto que sí hay diferencias en cuanto al nivel
de autoestima dependiendo de si han sufrido maltrato.

12. Tipos de colegio
y notas
Tenemos la siguiente tabla de contingencia que
refleja los datos de la asignatura de religión en
centro escolares. ¿Influye el tipo de colegio en la
nota obtenida? Con un margen de error 0,05.
H0. La nota de los dos colegios es igual o lo que es lo mismo, no hay
diferencia en la nota en relación al tipo de colegio.
H1. La titularidad del colegio influye en la nota de religión.

13. Tipos de colegio
y notas
Insuficiente Suficiente
o bien
Notable Sobresalien
te
Total
Centro
privado
6 14 17 9 46
Instituto 30 32 17 3 82
36 46 34 12 128
Variable independiente
- Centro privado
- Instituto
Variable dependiente
- Insuficiente
- Suficiente o bien
- Notable
- Sobresaliente
Insuficiente Suficiente o
bien
Notable Sobresalien
te
Total
Centro
Privado
36x46/128=
12,94
46x46/128=
16,53
34x46/128=
12,22
12x46/128=
4,31
46
Instituto 36x82/128=
23,06
46x82/128=
29,47
24x82/128=
15,38
12x82/128=
7,69
82
36 46 34 12 128
Tabla de frecuencias observadas
Tabla de frecuencias esperadas

14. Tipos de colegio
y notas
 𝑿 𝟐 =
(6−12,94)2
12,94
+
(14−16,53)2
16,53
+
(17−12,22)2
12,22
+
(9−4,31)2
4,31
+
(30−23,06)2
23,06
+
(32−29,47)2
29,47
+
(17−15,38)2
15,38
+
(12−7,69)2
7,69
= 𝟏𝟕, 𝟑
 GD = (4-1) . (2-1) = 3

15. Tipos de colegio
y notas
Sabiendo que el grado de libertad es 3,
miramos la tabla de distribución de X2
con nivel de significación del 95%. Este
valor es de 7,82.
Al ser menor que el valor de nuestra
X2, rechazamos la hipótesis nula,
afirmando por tanto que, el tipo de
colegio influye en la nota de religión,
ya que la diferencia observada no se
debe al azar.
17,3 > 7,82
Rechazamos la hipótesis nula. La diferencia es
estadísticamente significativa, por lo que podemos decir que
el tipo de colegio influye en la nota de religión, ya que la
diferencia observada no se debe al azar.

16. Dormir bien o
mal
En un grupo de enfermos que se quejaban de que
no dormían, se les dio somníferos y placebos.
Con un nivel de significación del 0,05.
H0. No hay diferencia para dormir bien o mal, si se toman somníferos
o placebos.
H1. Hay diferencia, y no es lo mismo tomar somníferos o placebos
para dormir bien o mal.
¿Es lo mismo tomar somníferos o placebos para
dormir bien o mal en este grupo de enfermos?

17. Dormir bien o
mal
Duerme bien Duerme mal
Somníferos 44 10 54
Placebos 81 35 116
125 45 170
Variable independiente
- Toma somníferos
- Toma placebos
Variable dependiente
- Duerme bien
- Duerme mal
Duerme bien Duerme mal
Somníferos 125x54/170=
39,71
45x54/170=
14,29
54
Placebos 125x116/170=
85,29
45x116/170=
30,71
116
125 45 170
Tabla de frecuencia observada
Tabla de frecuencia esperada

18. Dormir bien o
mal
 𝑿 𝟐 =
(44−39,71)2
39,71
+
(10−14,29)2
14,29
+
(81−85,29)2
85,29
+
(35−30,71)2
30,71
= 𝟐, 𝟓𝟖
 GL = (2-1) . (2-1) = 1

19. Dormir bien o
mal
Sabiendo que el grado de libertad
es 1, miramos la tabla de
distribución de X2 con nivel de
significación del 95%. Este valor es
de 3,84.
Al ser mayor que el valor de nuestra
X2, aceptamos la hipótesis nula,
afirmando por tanto que, no hay
diferencias para dormir bien o mal
si toman somníferos o placebos.
2,58 < 3,84
Aceptamos la hipótesis nula. No es estadísticamente
significativo, ya que es lo mimo tomar somníferos o
placebos para dormir bien o mal en ese grupo de enfermos.

20. SPSS con dos
variables
cualitativas
Realizar una tabla cruzada para calcular X2 en
SPSS. Para ello, seleccionamos dos variables
cualitativas.
H0. No hay diferencias en si enfermería fue la primera opción
en función del sexo.
H1. Sí hay diferencias en si enfermería fue la primera opción
en función del sexo.

21. SPSS con dos
variables
cualitativas
Variable independiente
- Sexo
Variable dependiente
- Fue enfermería tu primera
opción

22. SPSS con dos
variables
cualitativas
En la opción “estadísticos”
marcamos “Chi-cuadrado”.

23. SPSS con dos
variables
cualitativas

24. SPSS con dos
variables
cualitativas
El propio programa estadístico, nos
dice que la Chi-cuadrado de Pearson
no es la mejor manera de hallar el
valor de P, puesto que no cumple
con el requisito de tener un
recuento mayor o igual a 5.
Valor de P = 0,840 > 0,05
Aceptamos la hipótesis nula. No es estadísticamente
significativo, ya que no hay diferencia en si enfermería
fue la primera opción, en función del sexo.

25. Blanca Iglesias