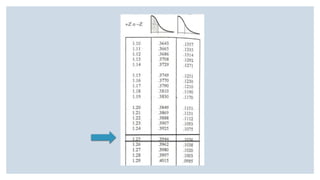
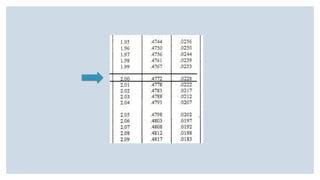
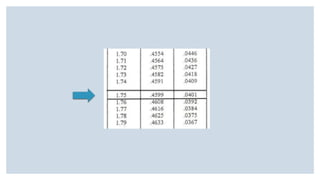
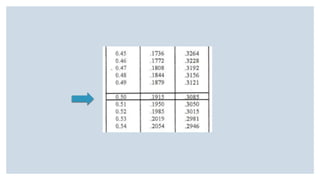
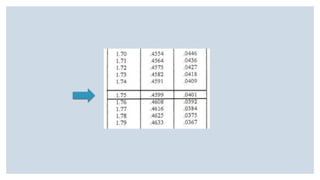
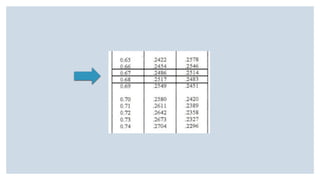
Este documento presenta varios ejercicios sobre tipificación de valores normales. Incluye ejercicios sobre la probabilidad de obtener una puntuación baja en una escala de autoestima, el porcentaje de adolescentes con diferentes niveles de estatura en Andalucía y la proporción de diabéticos con diferentes niveles de glucemia basal. Cada ejercicio calcula estas probabilidades y porcentajes usando la distribución normal y tablas de tipificación.

1. SEMINARIO 7
Tipificación valores normales
Blanca Iglesias

2. Ejercicios
◦ Ejercicios en casa para el blog sobre la escala de autoestima.
◦ Ejercicios sobre la altura de adolescentes en Andalucía.
◦ Ejercicios sobre la glucemia basal.

3. Ejercicios en casa para el blog sobre la
escala de autoestima
◦ ¿Cuál es la probabilidad de que una destinataria de asistencia
seleccionada al azar obtenga una puntuación de 10.5 o menos en la
escala de autoestima?

4. Ejercicios en casa
para el blog sobre
la escala de
autoestima
Como sabemos que la
media, la mediana y la moda
coinciden, el área que
queda bajo la gráfica es
simétrico a ambos lados de
µ=8, y tiene un valor de 0,5.
Por lo que sólo tenemos
que sumar el valor de la
tabla de tipificación normal
para Z=1,25, que era 0,3944,
más ese 0,5.

6. Ejercicios en
casa para el
blog sobre la
escala de
autoestima
Además, también podemos
hacerlo de forma que,
calculamos Z2 (que es el
área que queda bajo la
gráfica a la derecha de 10,5.
Z2 toma un valor de 0,1056.
Por lo tanto, a la unidad
total que representa la
gráfica, le restamos ese
valor.
La probabilidad de que una destinataria de asistencia seleccionada al azar
obtenga una puntuación de 10,5 o menos en la escala de autoestima es del
89,44%.

7. Ejercicios sobre la altura de adolescentes
en Andalucía
◦ Supongamos que la altura de adolescentes en Andalucía a los 10 años
sigue una distribución normal, siendo la media 140 cm y la desviación
típica 5 cm.
◦ ¿Qué porcentaje de niños tienen una talla menor de 150 cm?
◦ ¿Qué porcentaje de niños tienen una talla por encima de 150 cm?
◦ ¿Cuál es el porcentaje de niños con una talla comprendida entre 137,25 y 145,50
cm?

8. Ejercicios sobre
la altura de
adolescentes en
Andalucía
O bien calculamos el punto
Z (Z=2) y miramos su valor
(P=0,4772) en la tabla de
tipificación y le sumamos
0,5 (por las razones que
vimos anteriormente).
O, como ya también hemos
visto antes, podemos
restarle a la unidad el valor
de Z2 . Siendo en este caso
el valor de Z2 = 0.0228.
¿Qué porcentaje de niños tienen una talla menor de 150 cm?
El porcentaje de niños que tienen una talla menor de 150 cm es del
97,72%.

10. Ejercicios sobre
la altura de
adolescentes en
Andalucía
El valor de Z2 es de 0.0228.
Aunque también podemos
calcularlo, restándole al
100%, lo que calculamos en
el apartado anterior,
dándonos así el porcentaje
de niños con una talla
mayor de 150 cm.
¿Qué porcentaje de niños tienen una talla por encima de 150 cm?
El porcentaje de niños que tienen una talla por encima de 150 cm es del
2,28%.

11. Ejercicios sobre
la altura de
adolescentes en
Andalucía
En este caso, debemos de
calcular tanto Z1 (Z1=-0,55)
como Z2 (Z2=1,1) y sus
respectivos valores en la
tabla de tipificación (0,2088
y 0,3643).
En último lugar, sumamos
ambos valores para obtener
el porcentaje total de niños
con una talla comprendida
entre esos valores.
¿Cuál es el porcentaje de niños con una talla comprendida entre
137,25 y 145,50 cm?
El porcentaje de niños con una talla comprendida entre el 137,25 y 145,50
es del 57,31%.

13. Ejercicios sobre la glucemia basal
◦ La glucemia basal de los diabéticos atendidos en la consulta de enfermería debe
considerarse como una variable normalmente distribuida con media 106mg/100ml y
desviación típica de 8mg/100ml.
◦ Calcula la proporción de diabéticos con una glucemia basal inferior o igual a 120mg/100ml.
◦ La proporción de diabéticos con una glucemia basal comprendida entre 106 y110mg/ml.
◦ La proporción de diabéticos con una glucemia basal mayor de 120mg/100ml.
◦ El nivel de glucemia basal tal que por debajo de él están el 25% de los diabéticos, es decir, el
primer cuartil.

14. Ejercicios
sobre la
glucemia
basal
Calculamos el valor de Z1
(0,9599) para Z1=1,75. A este
valor le sumamos 0,5.
O también podemos
hacerlo, restándole a la
unidad el valor de Z2
(0,0401).
Calcula la proporción de diabéticos con una glucemia basal inferior o igual a
120mg/100ml.
La proporción de diabéticos con una glucemia basal inferior o igual a
120mg/100ml es de 95,99%.

16. Ejercicios
sobre la
glucemia
basal
Calculamos el valor (0,1915)
de Z para Z=0,5.
La proporción de diabéticos con una glucemia basal comprendida entre 106
y110mg/ml.
La proporción de diabéticos con una glucemia basal comprendida entre
106 y 110mg/100ml es de 19,15%.

18. Ejercicios
sobre la
glucemia
basal
Calculamos el valor (0,0401)
de Z2, que ya lo hicimos en
el primer apartado.
La proporción de diabéticos con una glucemia basal mayor de
120mg/100ml.
La proporción de diabéticos con una glucemia basal mayor de
120mg/100ml es de 4,01%.

20. Ejercicios
sobre la
glucemia
basal
Buscamos en la tabla los valores de
las probabilidades, no en la
columna Z, ya que en nuestro caso
conocemos el valor de la
probabilidad y necesitamos conocer
el valor de Z.
El valor 0,25 no es exacto en la
tabla. Lo valores mayor y menos
que él son 0,2514 al que le
corresponde un valor de Z de -0,67;
y 0,2483 al que le corresponde un
valor de Z de -0,68. El valor buscado
está entre los dos anteriores, de
forma que hacemos la media entre
ellos dos.
O sea, que -0,675 es el valor que
corresponde al primer cuartil de la
variable tipificada. Luego
calculamos el valor de la variable X,
que corresponde a ese valor y
despejamos X.
El nivel de glucemia basal tal que por debajo de él están el 25% de los
diabéticos, es decir, el primer cuartil.
El nivel de glucemia basal tal que por debajo de él están el 25% de los
diabéticos (primer cuartil), es de 100,6mg/100ml.

22. Blanca Iglesias