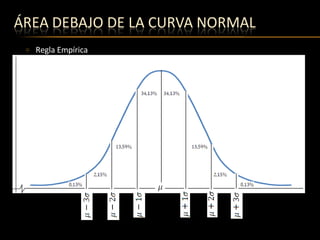
El documento habla sobre la curva normal y su uso para describir distribuciones de datos poblacionales. Explica que muchas variables de las ciencias del comportamiento siguen esta distribución y que pruebas de inferencia como z, t de Student y F requieren de ella. También describe cómo calcular puntajes z para determinar la posición de un valor dentro de la distribución y su percentil asociado, así como el cálculo de áreas bajo la curva.

1. Prof. Ricardo Escalante

2. BPMM30 2 3 4 5 La curva y sus interpretaciones La curva normal Ejercicios Puntajes z 1 6 Cálculo de punto percentil Área debajo de la curva normal

3. La curva normal es una distribución notable particularmente en las ciencias del comportamiento Un buen número de las variables que se someten a medición se ajustan aproximadamente a la curva normal Muchas pruebas en las cuales se infiere información requieren de una distribución muestral semejante a la curva normal. Los puntajes z , la t de Student y la F son pruebas de inferencia que requieren de este aspecto.

4. La curva normal es una distribución teórica de los datos de una población. Es una curva en forma de campana que se describe mediante la siguiente ecuación: El cálculo de cada punto de la curva como expresión de una frecuencia no será necesario, no obstante, se presenta la ecuación con el propósito de demostrar que la curva puede ser descrita en términos matemáticos.

5. Observe los puntos de inflexión de la curva Descritos como los puntos en los que la curva cambia y pasa de ser convexa a ser cóncava. Si la curva tiene forma de campana es una curva normal La curva es asintótica respecto al eje de las abscisas

6. Regla Empírica

7. Aplicación: Suponga que se aplica un test de CI a una población de 8000 personas. La distribución presenta una forma normal. De los cálculos estadísticos se obtiene  =102,  =12. Determine : La cantidad de personas con un CI comprendido entre 90 y 114 La cantidad de personas con un CI superior a 78 La cantidad de personas con un CI inferior a 126

8. Un puntaje z es un dato transformado que indica a cuántas unidades de desviación estándar, por exceso o por defecto de la media, se encuentra un dato en bruto En combinación con una curva normal, los puntajes z permiten determinar la cantidad de valores o el porcentaje de valores que se encuentran por encima o por debajo de cualquier dato en la distribución. Ejemplo: Supongamos que el índice académico acumulado de todos los estudiantes de la UNIMET está distribuido en forma normal , con  = 3,30 y  =0,55. ¿Cuál es el rango percentil de un estudiante cuyo IAA es de 4,40? ¿Cuál es el rango percentil de un estudiante cuyo IAA=2,75?

9. Un puntaje z es un dato transformado que indica a cuántas unidades de desviación estándar, por exceso o por defecto de la media, se encuentra un dato en bruto En combinación con una curva normal, los puntajes z permiten determinar la cantidad de valores o el porcentaje de valores que se encuentran por encima o por debajo de cualquier dato en la distribución. Ejemplo: Supongamos que los índices académicos acumulados de todos los estudiantes de la UNIMET están distribuidos en forma normal , con  = 3,30 y  =0,55. ¿Cuál es el rango percentil de un estudiante cuyo IAA es de 4,40? ¿Cuál es el rango percentil de un estudiante cuyo IAA=2,75? ¿Cuál es el puntaje z para un IAA=4,13?

10. ¿Cuál es el puntaje z para un IAA=4,13? Dado que la regla empírica no prevé esta situación y dada la necesidad de conocer el rango percentil para un puntaje de esta naturaleza , haremos uso de una tabla que ha sido elaborada para determinar el área bajo la curva correspondiente a distintos puntajes Z De esta manera el valor que corresponde para z=1,51 es Este sería el porcentaje de datos que se encuentran entre la media y el IAA=4,13. Si queremos calcular el rango percentil para X=4,13 debemos considerar los datos que se encuentran por debajo de la media, de manera que: 0,5000 + 0,4345= 0,9345 Lo que nos da un rango percentil de 93,45%

11. Las calificaciones de un examen nacional de aptitudes matemáticas presentan una distribución normal, con  = 80 y  =12. ¿Cuál es el rango percentil de una calificación de 84? ¿Qué porcentaje de las calificaciones se encuentra por debajo de una calificación de 66 puntos? ¿Qué porcentaje de calificaciones se encuentran entre 64 y 90? ¿Qué porcentaje de calificaciones se encuentran entre 95 y 110?

12. Determine el punto percentil correspondiente a 70% Calcule la distancia del punto al 50%. En este caso 70% - 50% =20% Determine mediante la tabla de puntajes z el porcentaje más cercano a 0,2000 Sustituya el puntaje z en la ecuación Efectúe el cálculo Determine el punto percentil correspondiente a 43% ¿Cuáles son los datos que marcan el 95% central de la distribución?