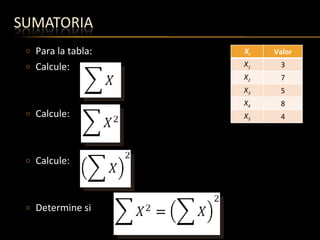
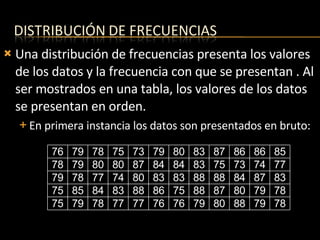
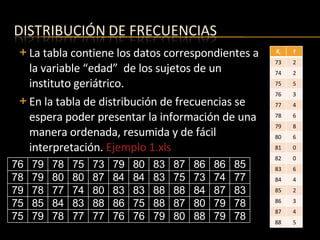
El documento presenta conceptos básicos de estadística como variables, sumatorias, distribución de frecuencias y tipos de variables. Explica cómo representar y resumir datos agrupados mediante tablas y define variables continuas y discretas. También cubre temas como redondeo de números y cálculo de sumatorias.

1. Prof. Ricardo Escalante

2. BPMM30 2 3 4 5 Notación matemática Sumatoria Redondeo y ejercicios Límites reales 1 6 Distribución de frecuencias Var. continuas y discretas

3. En estadística trabajaremos generalmente con datos agrupados obtenidos de la medición de una o más variables. Son más frecuentes los datos obtenidos con base en el estudio de muestras que los obtenidos de las mediciones aplicadas a los individuos de poblaciones. Utilizaremos las letras mayúsculas X, Y, Z, … para denotar las variables. En el caso de la medición de la edad de los sujetos podemos emplear X para representar la variable “edad”

4. Dado que la variable puede adoptar muchos valores agregaremos un subíndice a las variables con el propósito de distinguirlas. En este ejemplo X representa la variable “edad” N representa el número total de datos ( N=6) X i es el i-ésimo dato, donde i varia de 1 hasta N Número del sujeto Símbolo del dato Valor del dato, edad (años) 1 X 1 8 2 X 2 10 3 X 3 7 4 X 4 6 5 X 5 10 6 X 6 12

5. Una de las operaciones que vamos a realizar con mayor frecuencia en esta ciencia consiste en sumar los datos que conforman una distribución o una parte de los datos. Utilizaremos para denotar esta suma total o parcial a la letra griega mayúscula “ sigma” (  ) la cual indica la operación de sumatoria. Se lee como “ la suma de la variable X de i=1 a N ”

6. Al aplicar la sumatoria al cuadro de la distribución de las edades de 6 sujetos obtenemos: Número del sujeto Símbolo del dato Valor del dato, edad (años) 1 X 1 8 2 X 2 10 3 X 3 7 4 X 4 6 5 X 5 10 6 X 6 12

7. Si en la sumatoria se utilizan todos los datos ( de 1 a N ) pueden omitirse las notaciones colocadas arriba y abajo del signo de suma. Para el ejemplo anterior esto es equivalente a:

8. Para la tabla: La sumatoria del dato 2 hasta el dato 5 Para la siguiente tabla de datos: Determine: Número del sujeto Símbolo del dato Valor del dato, edad (años) 1 X 1 8 2 X 2 10 3 X 3 7 4 X 4 6 5 X 5 10 6 X 6 12 X i Valor X 1 20 X 2 24 X 3 25 X 4 28 X 5 31

9. Para la tabla: Calcule: Calcule: Calcule: Determine si X i Valor X 1 3 X 2 7 X 3 5 X 4 8 X 5 4

10. En la sesión N°1 se definió variable como: Variable: cualquier propiedad o característica de algún evento, objeto o persona, que puede tener diversos valores en diferentes instantes, según las condiciones. Igualmente se estableció la diferencia entre variable independiente y variable dependiente. Ahora distinguiremos entre variables continuas y discretas. Variable continua: teóricamente es aquella que puede asumir un número infinito de valores entre las unidades adyacentes de una escala. Variable discreta: es aquella para la cual no existen valores posibles ubicados entre las unidades adyacentes o consecutivas de una determinada escala.

11. Son aquellos valores que se encuentran por arriba y por debajo de los valores registrados a una distancia igual a la mitad de la unidad de la medida mínima de la escala utilizada. Ejemplos: El peso de una persona es de 97 Kg (menor unidad 1 Kg) entonces los límites reales serían 96,5Kg y 97,5Kg El peso de una persona es de 97 Kg (menor unidad 0,1 Kg) entonces los límites reales serían 96,95Kg y 97,05Kg

12. Divida en dos partes el número que desea redondear preservando el número de cifras decimales que desea conservar: (2 cifras decimales en este caso) 27,01761 27,01 (0,761) 27,02 27,01350 27,01 (0,350) 27,01 71,07500 71,07 (0,500) 71,08 71,06500 71,06 (0,500) 71,06 Si el residuo es mayor que 0,5 agregue una unidad al último digito decimal Si el residuo es menor que 0,5 deje el último dígito decimal sin cambios Si el residuo es igual a 0,5: Agregue 1 si el último dígito es impar No haga cambios si el último dígito es par

13. Ejercicios del 2 al 14 de las páginas 35 y 36 del libro de R. Pagano Determine la sumatoria 5b) 2,1 ; 3,2 ; 3,6 ; 5,0 ; 7,2 5d) 110; 112; 115; 120; 133 Redondee los siguientes números a dos cifras decimales: 6a) 14,53670 6b) 37,83500 6d) 46,50499 Calcule de la siguiente tabla: X i Valor X 1 37,28 X 2 21,097 X 3 17,6 X 4 43,11 X 5 7,003

14. Una distribución de frecuencias presenta los valores de los datos y la frecuencia con que se presentan . Al ser mostrados en una tabla, los valores de los datos se presentan en orden. En primera instancia los datos son presentados en bruto: 76 79 78 75 73 79 80 83 87 86 86 85 78 79 80 80 87 84 84 83 75 73 74 77 79 78 77 74 80 83 83 88 88 84 87 83 75 85 84 83 88 86 75 88 87 80 79 78 75 79 78 77 77 76 76 79 80 88 79 78

15. La tabla contiene los datos correspondientes a la variable “edad” de los sujetos de un instituto geriátrico. En la tabla de distribución de frecuencias se espera poder presentar la información de una manera ordenada, resumida y de fácil interpretación. Ejemplo 1.xls X i f 73 2 74 2 75 5 76 3 77 4 78 6 79 8 80 6 81 0 82 0 83 6 84 4 85 2 86 3 87 4 88 5 76 79 78 75 73 79 80 83 87 86 86 85 78 79 80 80 87 84 84 83 75 73 74 77 79 78 77 74 80 83 83 88 88 84 87 83 75 85 84 83 88 86 75 88 87 80 79 78 75 79 78 77 77 76 76 79 80 88 79 78